Calculating magnitudes from AS-1

seismograms (electronic version) 1

(L. Braile, June, 2004)

braile@purdue.edu

www.eas.purdue.edu/~braile

 

1.  Introduction:  This education module is designed to provide experience with seismograms and calculating magnitudes of earthquakes.  The seismograms that are provided were recorded by an AS-1 seismograph and the AmaSeis software.  This seismograph system is used in the IRIS Seismographs in Schools program (http://www.iris.edu/about/ENO/).  More information about the AS-1 seismograph and the AmaSeis software can be found at http://web.ics.purdue.edu/~braile/ (click on “AS-1 Seismograph Information”).  There are two versions of this lesson – one that uses the paper records (printed version) of the seismograms for interpreting and measuring amplitudes to calculate magnitudes, and one that uses the digital copies (electronic version) of the seismograms and the AmaSeis software to help the user interpret the seismograms and measure amplitudes.  Of course, to use the electronic version, the user must have access to a Windows computer and have the AmaSeis software installed on the computer.  Instructions for downloading, installing and using the AmaSeis software can be found at http://www.iris.edu/about/ENO/AS1AmaSeis.pdf and

http://web.ics.purdue.edu/~braile/edumod/as1lessons/UsingAmaSeis/UsingAmaSeis.htm.  In both versions of the calculating magnitudes lesson the magnitude calculations are performed using the online AS-1 magnitude calculator MagCalc.  If desired, the magnitude calculations can be performed “by hand” (usually with the help of an electronic calculator) using the formulas listed in the AS-1 magnitude document http://web.ics.purdue.edu/~braile/edumod/as1mag/as1mag3.htm.

 

Seismograms are records of ground motion (vibration or shaking of the ground) recorded by seismographs.  Thousands of seismograph stations are located around the world to monitor earthquake activity and detect and analyze records of explosions.  A world map showing the Global Seismograph Network (GSN) stations and recent earthquake activity can be viewed at http://www.iris.edu/seismon/.  Seismograms are used to locate earthquakes, determine the magnitude (size) of earthquakes and explosions, analyze seismic wave propagation, evaluate earthquake hazards, and study the structure of the Earth’s interior.

 

More information, including examples, on calculating magnitudes from AS-1 seismograms can be found in the online Magnitude Calculator, MagCalc

(http://web.ics.purdue.edu/~braile/edumod/MagCalc/MagCalc.htm) and at

http://web.ics.purdue.edu/~braile/edumod/as1mag/as1mag3.htm.  Detailed instructions for using the AmaSeis software are available at

http://web.ics.purdue.edu/~braile/edumod/as1lessons/UsingAmaSeis/UsingAmaSeis.htm and

http://www.scieds.com/spinet/. 

 

In addition to the web version of this document, MS Word and PDF versions are available at:

http://web.ics.purdue.edu/~braile/edumod/as1lessons/magnitude/CalcMagnElect.doc

http://web.ics.purdue.edu/~braile/edumod/as1lessons/magnitude/CalcMagnElect.pdf.

 

2.  Magnitude:  The magnitude of an earthquake is a measure of the size of the earthquake or the energy released.  Many magnitude formulas have been developed over the years.  Recently, the Moment Magnitude (Mw, now usually referred to as just Magnitude or M, such as for an “M8 earthquake”) formula and method is the preferred estimate and is routinely reported.  Richter magnitude was defined for California and is no longer the best magnitude formula for most earthquakes.  Despite the fact that seismologists use primarily the moment magnitude, earthquake magnitudes reported by the media are often called “Richter magnitude”.  Because the moment magnitude method requires recordings of very long period seismic waves (typically using modern and expensive, broadband digital seismographs), moment magnitude cannot be calculated from AS-1 seismograms.  However, other traditional magnitude formulas can be used.  These magnitude estimates (the body wave magnitude, mb; the surface wave magnitude, MS; and the mbLg wave magnitude, mbLg) can be readily calculated from AS-1 seismograms and provide useful estimates of the size of earthquakes.  Magnitude estimates using mb, MS and mbLg formulas are commonly reported for well-recorded earthquakes so one can compare the magnitude estimates from AS-1 seismograms with “official” magnitudes listed by the US Geological Survey.  To find these magnitude estimates for earthquakes listed on the Internet, see the instructions at

http://web.ics.purdue.edu/~braile/edumod/eqdata/eqdata.htm.  The magnitude estimates calculated from AS-1 seismograms are quite accurate as shown by comparisons with official USGS estimates (http://web.ics.purdue.edu/~braile/edumod/MagCalc/AS1Results.htm).  More information about earthquake magnitude can be found at the online sites listed in the Introduction and in Bolt (1993, 1999). 

 

To calculate magnitude from AS-1 seismograms, one needs to measure the amplitude (in digital units) of the appropriate phase or arrival (first, P arrival; surface wave; or Lg wave) and the period of the waves.  These measurements can be readily obtained from the seismograms using the AmaSeis software (see Using AmaSeis for more details) or by direct measurements from paper copies of the seismograms.  An example of amplitude and period measurements is shown in Figure 1 (for the P arrival and the mb magnitude).  The epicenter-to-station distance is also required because, for a given magnitude earthquake, the amplitude of wave arrivals decreases with distance from the epicenter.  This distance is usually given in geocentric angle (in degrees; for example the geocentric angle for an earthquake at the equator and a station at the North Pole would be 90o; to convert distance in degrees to distance in kilometers along the Earth’s surface, multiply the distance in degrees by 111.19 km/degree).  This distance can sometimes be estimated directly from the seismogram using the S minus P arrival time.  Alternatively, the distance can be calculated by knowing the locations (latitudes and longitudes) of the epicenter and the seismograph station.  For most of the seismograms given below, the distance is provided.  The amplitude, period and distance are input to the magnitude calculator (MagCalc) to determine the magnitude.  Additional information on calculating distance and on use of the magnitude calculator can be found in the Using AmaSeis document and in MagCalc. 

 

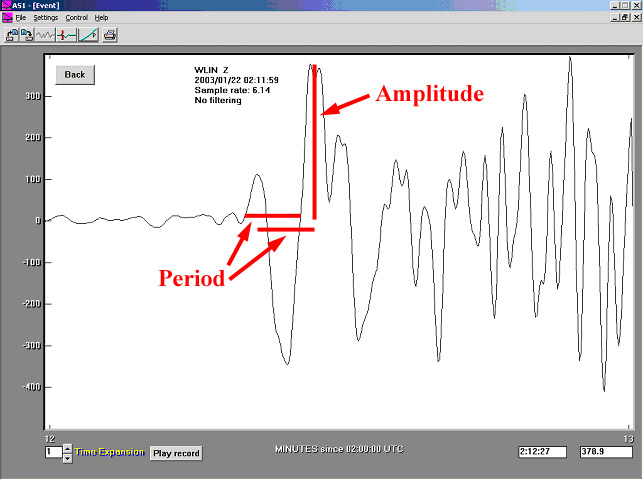
Figure 1.  Example of a seismogram (M7.8 Colima, Mexico earthquake, January 22, 2003) displayed using the AmaSeis software.  The view has been “zoomed in” by selecting (extracting) a small time duration to view the first (P) arrival.  The time scale (horizontal scale) shows one minute of the seismogram.  The vertical scale is relative amplitude in digital units.  The vertical bar illustrates the amplitude measurement for this arrival and indicates an amplitude of about 380 digital units.  The horizontal bars show two approaches to measuring the approximate period of the wave arrival.  The upper bar is drawn between 3 successive zero crossings of the signal defining approximately one cycle of the wave motion.  The lower bar is drawn between two successive peaks (or troughs) of the signal, also defining approximately one cycle of the wave motion.  For both methods, the measurements (length of the bars in seconds) indicate that the approximate period of the wave motion is 5 seconds.

 

3.  Sample seismograms for magnitude calculation:  Sample seismograms are provided below for calculation of magnitudes using the AmaSeis software to open, view and enlarge the seismogram, and measure the amplitude and period.  For the first 6 seismograms, the epicenter-to-station distance is provided.  For the remaining 3 seismograms, the epicenter to station distance can be estimated from the S minus P time (or calculated from the latitudes and longitudes of the epicenter and the station).  Calculations for the mb, MS and mbLg magnitudes can be performed using the seismograms listed below. All of the seismograms were recorded at AS-1 station WLIN (West Lafayette, IN, 40.484oN, 86.881oW).  For each seismogram, the magnitude, earthquake name, date, origin time, and epicenter location (latitude and longitude) are provided.  Copies of 24-hour screen displays from the AmaSeis program for the selected earthquakes are shown in Figures 2-10.

 

For one or more seismograms, download the SAC format seismogram to your computer (click on the appropriate “.sac” links below, and place in a folder called SAC Files within your AmaSeis Folder).  Open the seismogram in the AmaSeis program to view the record.  Enlarge the time range of interest (P arrival for the mb magnitude determination; 20-second surface wave arrival, commonly the largest of the surface waves, for the MS magnitude determination; Lg arrival, almost always the largest arrival for distances of 0-30 degrees for shallow earthquakes, for the mbLg magnitude determination). Use the amplitude tool (place cursor at the maximum amplitude of the selected phase and read the amplitude in the window in the lower right hand corner of the screen) to determine the amplitude.  Be sure that the “zero line” is approximately at zero amplitude; if not the zero-line amplitude must be subtracted from the amplitude of the maximum signal.  The cursor can also be used to measure the period using either of the approaches illustrated in Figure 1.  The times of the two locations on the waves (see examples in Figure 1; between two peaks or troughs, or 3 successive zero crossings) can be read from the cursor time window (just left of the amplitude window) and subtracted to provide an estimate of the wave period.  Enter the amplitude, period and distance into the appropriate magnitude tool in the magnitude calculator (MagCalc) to determine the magnitude estimate for the recorded earthquake.  Compare the magnitudes that you calculate from the AS-1 seismograms with the official magnitude (for mb, MS or mbLg magnitude estimates; Figure 11).  Select some questions (see section 4 below) to answer related to your seismograms and earthquakes.

 

3.1.    Body wave magnitude (mb), Example 1:  M7.8 Colima, Mexico earthquake, January 22, 2003, 02:06:36 UTC, 18.81oN, 104.50oW, epicenter-to-station distance = 26.01o.

http://web.ics.purdue.edu/~braile/edumod/as1lessons/magnitude/Colima30minute.sac

 

 

3.2.    Body wave magnitude (mb), Example 2:  M6.5 San Simeon, California earthquake, December 22, 2003, 19:15:56 UTC, 35.706oN, 121.102oW, epicenter-to-station distance = 27.24o.

http://web.ics.purdue.edu/~braile/edumod/as1lessons/magnitude/SanSimeon30minute.sac

 

 

3.3.    Surface wave magnitude (MS), Example 1:  M8.1 Hokkaido, Japan earthquake, September 25, 2003, 04:45:36 UTC, 41.827oN, 143.830oE, epicenter-to-station distance = 86.07o.

http://web.ics.purdue.edu/~braile/edumod/as1lessons/magnitude/Hokkaido60minute.sac

 

 

3.4.    Surface wave magnitude (MS), Example 2:  M7.2 South Island, New Zealand earthquake, August 21, 2003, 12:12:50 UTC, 45.154oS, 167.179oE, epicenter-to-station distance = 127.240o.

http://web.ics.purdue.edu/~braile/edumod/as1lessons/magnitude/NewZealand60minute.sac

 

 

3.5.    Lg wave magnitude (mbLg), Example 1:  M4.4 Evansville, Indiana earthquake, June 18, 2002, 17:37:14 UTC, 37.985oN, 87.778oW, epicenter-to-station distance = 2.590o.

http://web.ics.purdue.edu/~braile/edumod/as1lessons/magnitude/Evansville5minute.sac

 

 

3.6.    Lg wave magnitude (mbLg), Example 2:  M4.6 NE Alabama earthquake, April 29, 2003, 08:59:38 UTC, 34.508oN, 85.612oW, epicenter-to-station distance = 6.050o.

http://web.ics.purdue.edu/~braile/edumod/as1lessons/magnitude/NEAlabama5minute.sac

 

 

3.7.    Body wave magnitude (mb), estimate distance from S minus P time, Example 1:  M6.7 Central Alaska (Denali fault) earthquake, October 23, 2002, 11:04:20 UTC, 63.576oN, 148.088oW.

http://web.ics.purdue.edu/~braile/edumod/as1lessons/magnitude/Denali30minute.sac

 

 

3.8.    Surface wave magnitude (MS), estimate distance from S minus P time, Example 1:  M6.6 Unimak Island, Alaska earthquake, February 19, 2003, 03:32:36 UTC, 53.870oN, 164.650oW.

http://web.ics.purdue.edu/~braile/edumod/as1lessons/magnitude/UnimakIsland30minute.sac

 

 

3.9.    Body and surface wave magnitude (mb, MS), estimate distance from S minus P time, Example 1:  M6.8 N. Algeria earthquake, May 21, 2003, 18:44:19 UTC, 36.876oN, 3.727oE.

http://web.ics.purdue.edu/~braile/edumod/as1lessons/magnitude/NAlgeria60minute.sac

 

 

4.  Questions and extensions:  Below are some questions (including some “challenge questions”) and some suggested enrichment activities that are related to seismograms, magnitude and earthquake activity. 

 

4.1.  Find the location of your selected earthquakes on a map or globe.  What type of plate boundary is present in the areas of the earthquakes? 

 

4.2.  Perform a web search to find information about damage for some of the larger earthquakes listed above.  What damage and injuries were reported?  Why might some moderate sized earthquakes cause significant damage while some very large earthquakes are not associated with significant damage?

 

4.3.  Examine the Hokkaido earthquake seismogram.  By enlarging the appropriate arrivals on the seismogram and using the time window displaying the time corresponding to the cursor location (or the time scale at the bottom of the screen), estimate the periods of the waves for the first P arrival, S arrival and surface wave arrivals.

 

4.4.  Compare the seismograms for the Colima and San Simeon earthquakes.  These earthquakes were approximately the same distance from the seismograph station (WLIN) but had very different magnitudes.  What features of the seismograms (position in time of the main arrivals, amplitude and period of the arrivals) are similar?  What features are different?  Suggest an explanation for your observations.

 

4.5.  Examine the New Zealand earthquake seismogram which displays very prominent surface waves.  How long did it take for the surface waves to travel from the epicenter to the seismograph station (travel time = arrival time – origin time; use the arrival time of the largest amplitude of the surface waves?  What is the approximate average velocity (in km/s) that these waves traveled?

 

4.6.  Compare the seismograms for the San Simeon, Central Alaska and Unimak Island earthquakes.  These earthquakes were approximately the same magnitude (6.5, 6.7, and 6.6) but were different distances from the recording station (WLIN).  What features of the seismograms (position in time of the main arrivals, amplitude and period of the arrivals, duration of wave energy) are similar?  What features are different?  Suggest an explanation for your observations.

 

4.7.  question for Evansville and NE Ala event pick s-p est dist from t-x or interpolate from table calc dist in km

 

Delta Time of P  S-P Time
Deg   M   S     M   S
0.0   0   5.4   0   4.0
0.5   0  10.6   0   7.8
1.0   0  17.7   0  13.5
1.5   0  24.6   0  19.0
2.0   0  31.4   0  24.4
2.5   0  38.3   0  29.9
3.0   0  45.2   0  35.4
3.5   0  52.1   0  40.9
4.0   0  58.9   0  46.4
4.5   1   5.8   0  51.9
5.0   1  12.7   0  57.4

 

4.8.    calculate mb for San Simeon EQ using WLIN and ASAZ.  Note very different amplitudes (primarily due to difference in distance) on seismograms.  Mb formula accounts for this expected difference. Compare mb calculated from the two stations.

 

extension/challenge PP,SS etc, Yukon event  http://web.ics.purdue.edu/~braile/edumod/as1lessons/magnitude/SYukon20minuteFiltered.sac

 

 

extensions/challenge Spinet (also other M7+)

 

extensions/challenge find other events

 

5.  Teaching strategies:  Teachers can use this teaching module in a variety of ways depending on the background of their students (in the use of computers and experience with earthquake-related information), the availability of computers in the classroom or school, and the amount of time that the teacher wishes to devote to the lesson.  If sufficient computers are available (at school or home) the teacher can have students or student teams perform the activities (analyze the seismograms and calculate a few or all of the magnitudes and answer selected questions) independently.  Alternatively, one could use the workstation or centers approach by setting up one or two computers in the room with the required software and data and have students rotate through the centers and complete some of the magnitude calculations and answer selected questions.  Using this approach, it is useful to have “lead student” with higher ability and interest in computers or the subject serve as a trainer or technical resource for the student teams visiting the center.  Finally, the teacher can lead the entire class or groups of students through the lessons using the interactive demonstration and exploration approach, first illustrating the software and the data and then performing the interpretation and magnitude calculation activities and answering selected questions with the participation of the students.  This approach works best with your computer attached to an LCD projector but can also be effective with a group of students gathered around a single computer display.  Comparing the results of student’s interpretations of the seismograms (amplitude, period, etc.) and calculated magnitudes with the correct answers, and correctly answering the questions chosen by the teacher provide an excellent assessment of student learning.

 

Before using this activity, students should have some understanding of earthquakes, plate tectonics and seismic wave propagation.  Studies of Earth structure could be performed either before or after this activity.  Appropriate information on these topics is contained in Bolt (1993, 1999).  Activities related to these topics are available at www.eas.purdue.edu/~braile.  The seismic wave activity using the slinky is particularly appropriate.  The calculating magnitude activity is especially useful for classrooms running an AS-1 seismograph as the students can use their experience to interpret seismograms recorded by their AS-1 and routinely calculate earthquake magnitudes.

 

6.  Connection to teaching standards:  Connections of the calculating magnitudes activities and materials to the National Science Education Standards (1996) are shown in Table 1.

 

Table 1.  “Calculating Magnitudes” and the National Science Education Standards (NSES).

NSES Standard

How standard is addressed by calculating magnitudes activities and materials*
Science Teaching Standards

Activities are inquiry-based (A, B) and provide opportunities for assessment using questions provided (C).
Professional Development Standards

Activities provide opportunities and resource material for teachers to learn about an Earth science topic that is not likely to have been included in their previous educational experiences (A, C) and include suggestions for effective teaching strategies (B).

Assessment Standards

Authentic assessment activities and questions for assessing achievement in learning key concepts are included (C).
Science Content Standards

 

-          Unifying Concepts and   

      Processes in Science

Activities provide experience with observation, evidence and explanation, and constancy, change and measurement.

-     Science as Inquiry

Activities provide opportunities for practice of inquiry and of fundamental science skills (Grades 5-8 and 9-12, A).

-     Physical Science Standards

Activities explore properties and changes of properties in matter, motion and forces, transfer of energy (Grades 5-8, B).

Activities explore structure and properties of matter, motions and forces, and interactions of energy and matter (Grades 9-12, B).

-          Earth and Space Science

-          Science in Personal and Social Perspectives

Activities relate to energy in the Earth system (Grades 9-12, D).

Activities explore natural hazards (Grades 5-8, F; Grades 9-12, F).

Science Education Program Standards

Seismogram and magnitude activities are developmentally appropriate, interesting and relevant, and emphasize student understanding through inquiry, and are connected to other school subjects (B).

Seismogram and magnitude activities provide practice with mathematics and analysis skills (C).

Science Education System Standards

Because the software, data and materials necessary to perform the seismogram and magnitude activities are free and available on the Internet, they are easily accessible to all students.

*Letters in parentheses identify specific standards within the six areas (Science Teaching, Professional Development, Assessment, Science Content, Science Education Programs, and Science Education System Standards) of the NSES.

 

7.   References:

 

Bolt, B.A., Earthquakes and Geological Discovery, Scientific American Library, W.H. Freeman,

New York, 229 pp., 1993.

 

Bolt, B.A., Earthquakes, (4th edition), W.H. Freeman & Company, New York, 364 pp., 1999.

 

National Research Council, National Science Education Standards, National Academy of Sciences,

            Washington, D.C., 262 pp., 1996.

 

8.  Earthquake recordings (24-hour screen displays) and table of earthquake information:

 

Reference AS-1 on SpiNet http://www.earthscope-eon.org/spinet/ http://www.iris.edu/about/ENO/AS1AmaSeis.pdf

Reference accessing data http://web.ics.purdue.edu/~braile/edumod/eqdata/eqdata.htm

Reference as1 links and install page lwb http://web.ics.purdue.edu/~braile/ http://web.ics.purdue.edu/~braile/edumod/as1mag/as1mag.htm

http://web.ics.purdue.edu/~braile/indexlinks/as1.htm

Also technical assistance and a tutorial under the Help menu in AmaSeis

 

Slinky

 

http://web.ics.purdue.edu/~braile/edumod/slinky/slinky.htm

http://web.ics.purdue.edu/~braile/edumod/slinky/slinky.doc

http://web.ics.purdue.edu/~braile/edumod/slinky/slinky4.htm

http://web.ics.purdue.edu/~braile/edumod/slinky/slinky4.doc


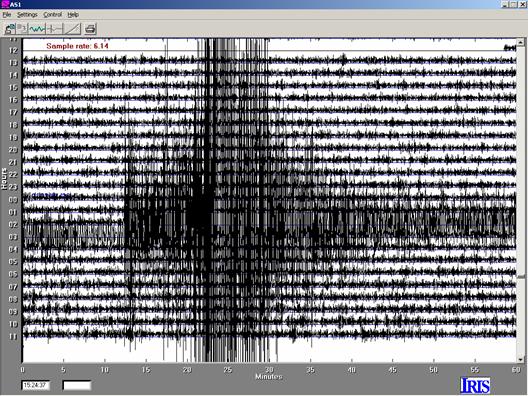
Figure 2.  24-hour AmaSeis record for seismogram 3.1, M7.8 Colima, Mexico earthquake, January 22, 2003.

 

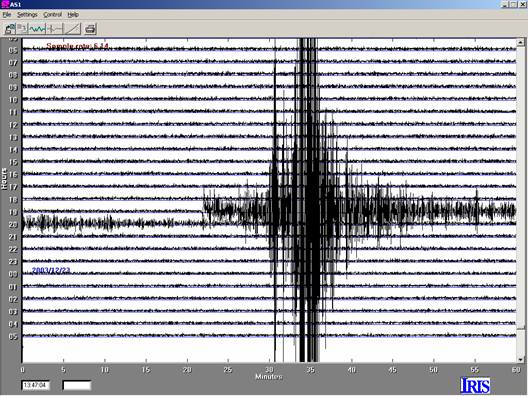
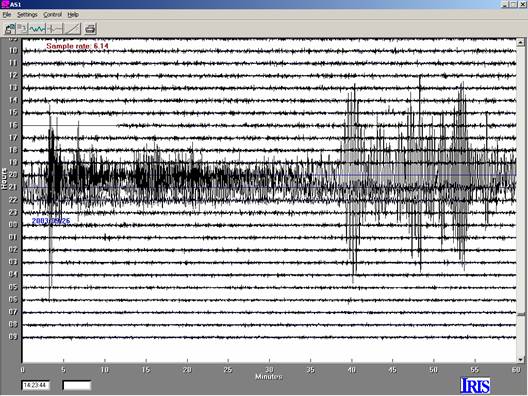
Figure 3.  24-hour AmaSeis record for seismogram 3.2, M6.5 San Simeon, California earthquake, December 22, 2003.

 

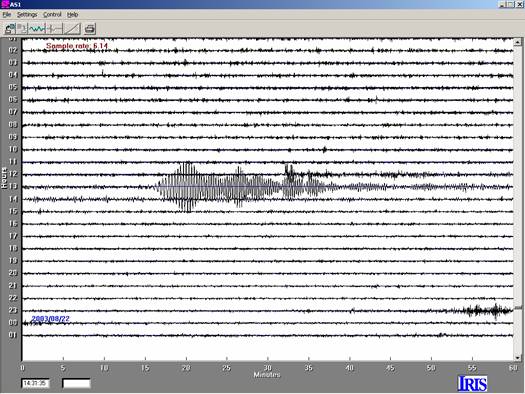
Figure 4.  24-hour AmaSeis record for seismogram 3.3, M8.1 Hokkaido, Japan earthquake, September 25, 2003.

 

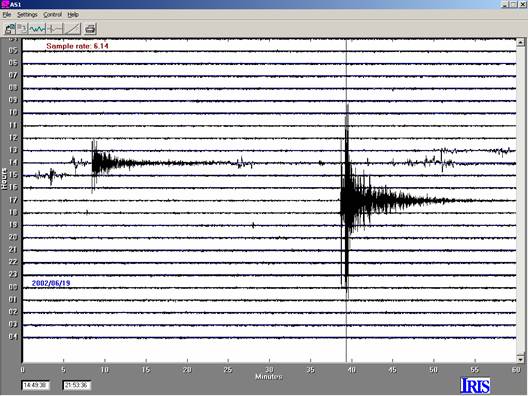
Figure 5.  24-hour AmaSeis record for seismogram 3.4, M7.2 South Island, New Zealand earthquake, August 21, 2003.

 

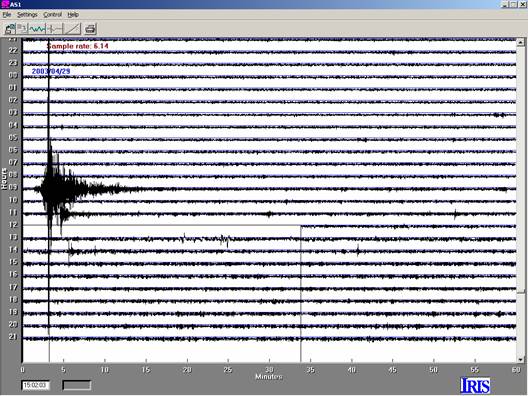
Figure 6.  24-hour AmaSeis record for seismogram 3.5, M4.4 Evansville, Indiana earthquake, June 18, 2002.

 

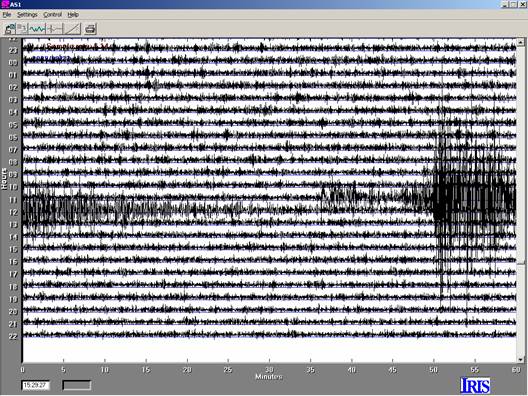
Figure 7.  24-hour AmaSeis record for seismogram 3.6, M4.6 NE Alabama earthquake, April 29, 2003.

 

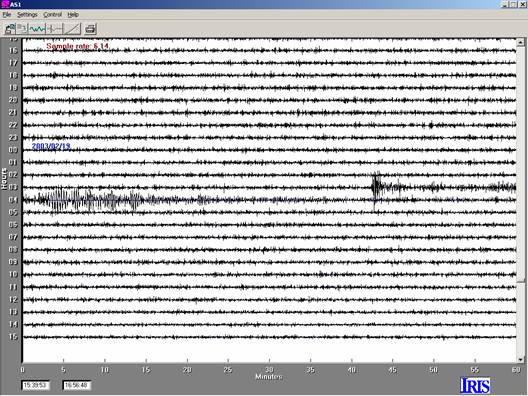
Figure 8.  24-hour AmaSeis record for seismogram 3.7, M6.7 Central Alaska (Denali fault) earthquake, October 23, 2002.

 

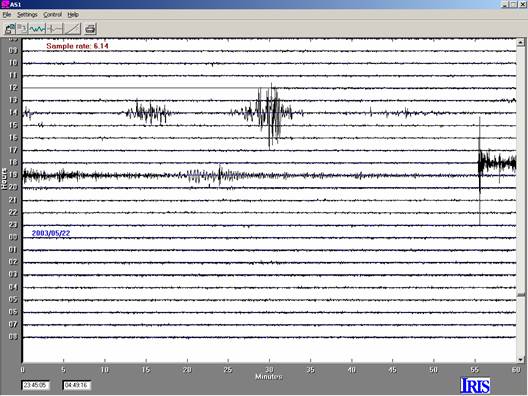
Figure 9.  24-hour AmaSeis record for seismogram 3.8, M6.6 Unimak Island, Alaska earthquake, February 19, 2003.

 

Figure 10.  24-hour AmaSeis record for seismogram 3.9, M6.8 N. Algeria earthquake, May 21, 2003.

 

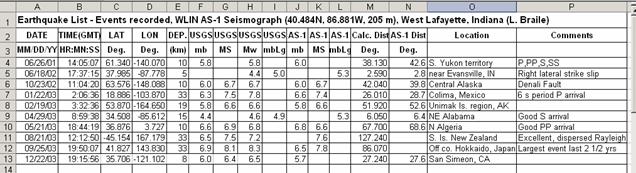
Figure 11.  Table of information for the earthquakes and seismograms used in this teaching module.

 

 

 

AS-1 Seismograph Links: www.eas.purdue.edu/~braile/ (click on “AS-1 Seismograph Information”)

List of AS-1 Teaching Modules: www.eas.purdue.edu/~braile/edumod/as1lessons/as1lessons.htm

 

[1]                     Last modified November 21, 2004

The web page for this document is: http://web.ics.purdue.edu/~braile/edumod/as1lessons/magnitude/CalcMagnElect.htm.  

Funding for this development provided by IRIS and the National Science Foundation.

ă Copyright 2004.  L. Braile.  Permission granted for reproduction for non-commercial uses.