Earth’s
Interior Structure - Seismic Travel Times in a Constant Velocity Sphere
(L. BraileÓ, December, 2000)
http://web.ics.purdue.edu/~braile
|
|
Introduction:
Using simple calculations of the
travel times of seismic waves in a constant velocity, spherical Earth and
comparison of the travel times with observations for the real Earth, we find
that the Earth’s interior is not homogeneous.
Examination of the travel time data and calculations provides
suggestions about the actual nature of the Earth’s interior structure.
Educational Objective: Provide experience with graphing, calculations and graphical analysis. Infer the structure of the Earth’s interior and gain experience with the methods used to study Earth structure. Optionally, provide an opportunity to make calculations using a calculator from an equation, or to write a computer program to perform seismic travel time calculations.
Possible Preparatory Lessons/Activities:
Seismic wave propagation
Elasticity
Materials:
2 11” x 17” sheets of photocopy paper
metric ruler
calculator
pencil or pen
40 cm long piece of string
protractor
scotch tape
copies of figures
Procedure:
1. Draw a cross section of half of the spherical Earth using a scale of 1:25,000,000 on the two sheets of paper taped together along the long side (Figure 1). Use the string with a loop at one end to draw the semi-circle arc with a radius of 25.5 cm to represent the Earth’s surface in the cross section diagram. Alternatively, a template (Figure 2) is provided to make the half-sphere model. Copy the template (one half of figure at a time onto an 11x17 piece of paper using 200% enlargement. The two halves can then be taped together.
2. Draw raypaths associated with geocentric angles (a measure of distance from a source [earthquake] to a receiver [seismograph station]) of 40°, 80°, 120°, 150° and 180°. Use the protractor to measure the angles. One angle and raypath is shown in Figure 1 as an example.
3. Measure the distance (in cm, using the metric ruler) from source to receiver along the raypaths for each of the angles and write the result in Table 1. Convert these measurements to units of km for the real Earth by multiplying by 250 (accounting for our scale factor of 1 cm = 250 km or 1:25,000,000 in the scale model diagram) and write these numbers in the third column of the table. Determine the travel times for each raypath assuming a constant velocity of 11 km/s (divide length of raypath in km by velocity in km/s). Convert these times to minutes by dividing by 60. (These calculations could have been made more precisely by deriving a formula for the length of a chord of a circle using the geometry illustrated in Figure 3. However, the graphical solution is adequate to illustrate the concept of travel times through the Earth and is more concrete. We will use the formula which follows from the diagram in Figure 3 in the calculation of travel times using a computer program. You could also try other constant velocities, such as 10 km/s or 12 km/s, to see if the calculated travel times better fit the observed data.)
Table 1.
Calculation of travel times for raypaths in a spherical, constant
velocity Earth at various distances (geocentric angle).
|
|
Angle D (degrees) |
Length of Raypath measured on diagram (cm) |
raypath length (km) |
Time (s) |
Time (min) |
|
|
|
40 |
|
|
|
|
|
|
|
80 |
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
150 |
|
|
|
|
|
|
|
180 |
|
|
|
|
|
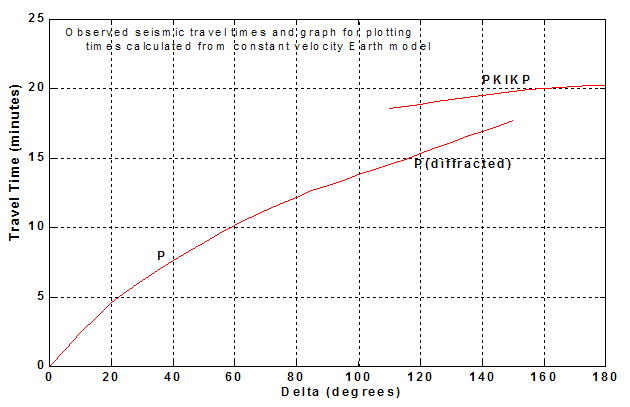
4. Plot the calculated travel times at the five distances (place a dot at the distance and location given by the data in columns 1 and 5 of Table 1 on the graph shown in Figure 4. Draw a smooth curved line through the calculated travel times (from the graphical calculations, Table 1) beginning at zero distance (Delta) and zero time. Observed travel times for the compressional wave are plotted as solid lines. These lines correspond to three different phases (different paths through the Earth), but for now are simply used for a comparison with the calculated times. Do the observed and calculated times differ significantly? What does this imply about our assumption that the Earth’s interior might consist of a constant velocity of 11 km/s?
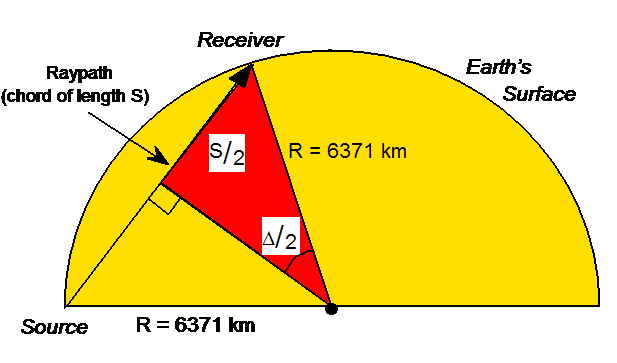
5. We can calculate the travel times in a homogeneous Earth more precisely (and thus compare observed and calculated travel times at all distances) using an equation corresponding to the geometry shown in Figure 3.
From the shaded triangle in the diagram in Figure 3, we have
![]() (1)
(1)
or,
![]() (2)
(2)
(R and S are in kilometers and D is in degrees)
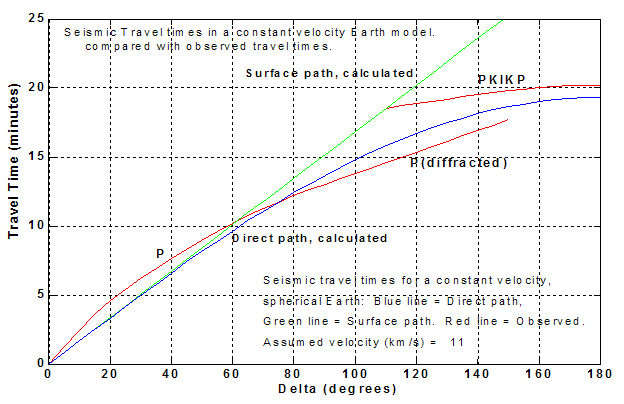
from which the length of the raypath can be calculated for any distance (geocentric angle), D. The travel times for a constant velocity Earth can then be calculated by dividing by the assumed velocity. In order to compare the observed travel times with other possible raypaths, we also calculate the travel times for the path along the surface of the homogeneous Earth. For this path, the distance is just D in degrees, or D multiplied by 111.19 km/degree to obtain the distance in km, which can be used to determine travel time by dividing by velocity. A computer program (Table 2) to calculate and plot the travel times was prepared using MATLAB* . The calculations could be made by writing a program in any computer language. The results of the calculations from the program are illustrated in a travel time graph (Figure 5) and in the tabular output of the program (Table 3).
Questions:
Examine the observed and calculated travel times shown on the graph (Figure 5) and answer the following questions.
1. Do the observed travel times differ significantly (discuss what differ significantly means in this analysis; compare differences with the expected experimental error in the travel times) from the calculated times for the surface and direct paths? (The time of arrival of seismic waves at a seismograph station can usually be determined with an accuracy of better than 1 second.)
2. If the Earth is homogeneous but we selected a different velocity than 11 km/s, could we obtain an adequate fit between the observed and calculated travel times? Why or why not? (Note that we could easily try many different velocities using the graphical solution, calculations using a calculator and the formula given above for determining the raypath length, S, or by using the computer program.)
3. Now that we know that the Earth’s interior cannot consist of a constant velocity, we use the travel time information to make additional inferences about the velocity structure of the interior. Examine the raypaths that you constructed using the graphical analysis. By comparing the distance ranges where the observed and calculated travel times (for the P and P diffracted phases) differ significantly in Figure 5 with the “depth penetration” of the corresponding raypaths in the hand-plotted graph, can you infer the relative velocity (compared to our 11 km/s assumption) of the actual Earth’s interior for the shallow (about 0 to 1500 km depth) and deeper (greater than 1500 km depth) regions of the Earth? In other words, is the assumed constant velocity of 11 km/s too high or too low for the shallow or deep Earth?
4. What causes the travel time curves to “flatten” so strongly in the distance range of about 160 to 180 degrees?
5. From the simple analysis that we have performed, we can infer that Earth’s interior has a velocity structure in which the velocity varies with depth. How could we determine if the velocity also varies laterally (with location)?
Additional Information:
1. Examine Chapter 6 of Bolt (1993) to learn more about the actual velocity structure of the Earth’s interior and how this information has been obtained, both historically and utilizing modern and much more extensive observations and techniques.
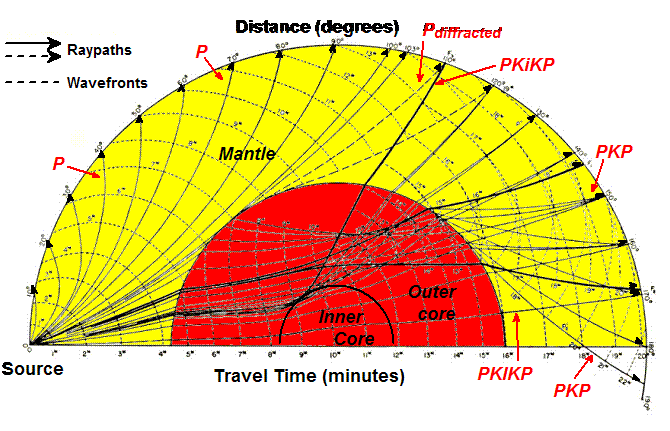
2. The raypaths for compressional waves in a more accurate Earth model are shown in Figure 6.
Possible Follow-Up Lessons/Activities:
Earth’s Interior Structure (Scale model “slice” through the Earth)
Reflection and Refraction
SEISMIC WAVES Program
Earthquake location techniques
References:
Bolt,
B.A., Earthquakes and Geological
Discovery, Freeman,
Richter,
C.F., Elementary Seismology, Freeman,
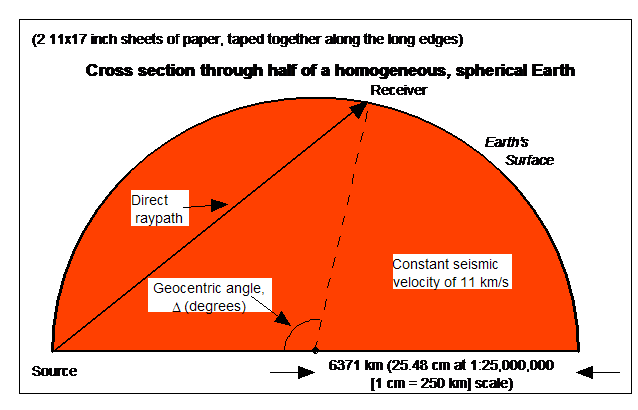
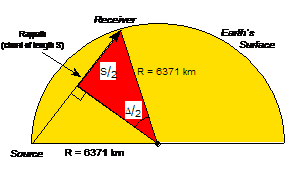
Figure 1. Cross section through half of a homogeneous,
constant seismic velocity, spherical Earth.
Sample seismic raypath from a surface source to a receiver at a distance
of D degrees geocentric angle (one degree corresponds to 111.19 km,
measured along the surface, for a 6371 km sphere) is shown by the heavy
line. For a graphical construction of
this model and measuring the distance along raypaths corresponding to various
geocentric angles (distances), the half circle can be drawn at a scale of
1:25,000,000 on two sheets of 11x17 inch paper taped together.