Walk - Run Activity --An S and P Wave Travel Time Simulation
(“S minus P”
Earthquake Location Method)
L. W. Braile
and S. J. Braileã
(June, 2000)
http://web.ics.purdue.edu/~braile
Objectives:
To model how earthquake waves travel through the Earth at different speeds.
To construct and utilize a graph to characterize the relationship between distance and time of travel of seismic waves (a travel time-curve).
To use the constructed time-travel graphs to locate the epicenter of a simulated earthquake by triangulation.
(The S and P wave propagation simulation and S minus P time earthquake location technique can be performed using either of two approaches -- the Walk – Run method, in which S wave propagation is simulated by walking and P wave propagation is simulated by running, or the Slow Walk – Walk method, in which S wave propagation is simulated by slow walking (small steps, about the length of one’s foot, or “heel-toe” walking) and P wave propagation is simulated by walking. The Walk – Run method can be performed on a playfield or a gymnasium and requires an “open space” of about 30 x 30 meters. The Slow Walk – Walk method can be performed in a medium sized room such as a classroom and requires an “open space” of about 6 x 6 meters. In the description that follows, and in the accompanying tables and figures, the Walk – Run instructions, labels and numbers are provided, and the Slow Walk – Walk information is given in brackets [].)
Materials:
Meter wheel (or a piece of rope 30 meters long marked at ten meter intervals), [or meter stick for Slow Walk – Walk method]
Stopwatches (3)
Handout with data tables
Playground or field at least 30m x 30m [or room with 6m x 6m space available for Slow Walk – Walk method]
Flags or other markers (4) to mark beginning and end of travel distance, seismograph recording stations and the location of the simulated earthquake, [masking tape]
Graph paper (or copies of Figures 1 and 2) and compasses
Calculator
Ruler/Straight-edge
Pencils (or colored pencils)
Procedure:
Part One:
Constructing the Travel-Time Graph
1. Explain to students that they are going to model the different speeds of P and S waves as they travel from the epicenter of an earthquake. Distribute handouts (data tables) and tell students that the procedure is in two parts. Indicate where the data for part One are to be recorded on Data Table 1.
2. Outdoors, establish a location where students may run without obstacles, in a straight line for 30 meters. [For the Slow Walk – Walk method, a room with at least 6 x 6 meters of open space will work.]
3. Measure a 30 meter distance, using a meter wheel or a pre-cut length of rope that is 30 meters long, and station a student with a stopwatch at 10 meters, one at 20 meters and one at 30 meters. [For the Slow Walk – Walk method, mark off a 6 meter line and put a mark at 0, 2, 4, and 6 meters. Masking tape on the floor is a convenient method for marking the line. The timers should be located at the 2, 4 and 6 meter marks.]
4. Establish a "cadence" for three students who will Walk [or Slow Walk] to simulate the travel speed of S waves. At "go" have the students Walk [or Slow Walk] to that cadence to the end of the 30 [6] meter distance. Have the timers record the length of time, in seconds, that it takes for the Walking [or Slow Walking] students to pass their station. Repeat this step, and record the length of time on Data Table 1. The students should try to Walk [or Slow Walk] at the same speed each time. Be sure that the results from the two trials produce similar times. Additional trials can be performed to provide additional data comparisons or to include more students in the experiment.
5. Establish a Running [or Walking] speed for three different students who will represent P waves. At "go" have these students Run [or Walk] from the same location to the three timers who will measure the length of time, in seconds, it took for the Runners [or Walkers] to pass their stations, and record it on the Data Table 1. Repeat this step, and record the length of time on the table. The students should try to Run [or Walk] at the same speed each time. Be sure that the results from the two trials produce similar times. Additional trials can be performed to provide additional data comparisons or to include more students in the experiment.
6. Return to classroom to analyze data and discuss the relationship of what they modeled to the way earthquake waves travel through the Earth. Direct the students to average the data for the two trials for Running [or Walking] times and Walking [or Slow Walking] times, and put data on the board for all to share. Then students will construct a graph (Figure 1) with distance in meters on the x-axis, and time in seconds on the y-axis, using different colored pencil lines (or the symbols and line patterns shown in the upper left corner of Figure 1) for the Walk [or Slow Walk] times, Run [or Walk] times, and Walk minus Run [or Slow Walk minus Walk] times. Sample data for the Slow Walk – Walk method are shown in Figure 4. Plot the points using the appropriate symbols and draw a straight line that approximately fits the data points. (Use Figure 1 and the appropriate scales for the Walk – Run or the Slow Walk – Run method [in brackets] to construct the graph of travel times. This travel time curve is just like the travel time curves that are used to determine the speeds of seismic waves in the Earth. The travel time curves are necessary to “calibrate” the distance calculation in the triangulation method that will be used in Part Two. This triangulation technique is often used to locate earthquakes from seismograms from three or more seismograph stations using the S and P arrival times, specifically, the S minus P times.)
Questions for students after they draw
their graphs:
1. "If you pick any point on the graph you have constructed for the Walking [or Slow Walking] time or Running [or Walking] time, what does that point represent?" (the time it takes to travel that particular distance; dividing distance by time determines the speed or velocity of travel to that distance)
2. "What is the speed of the Walking [or Slow Walking] students (representing S wave propagation) in m/s?" (divide distance by travel time to that distance for any of the stations or calculate the inverse slope of the line; approximately 1 to 2 m/s [0.3 to 0.8 m/s for Slow Walking])
3. "What is the speed of the Running [or Walking] students (representing P wave propagation) in m/s?" (divide distance by travel time to that distance for any of the stations or calculate the inverse slope of the line; approximately 3 to 4 m/s [1 to 2 m/s for Walking])
4. Compare these speeds to the speeds of P and S waves (P-waves travel about 6000-8000 m/s (6-8 km/s) and S-waves about 3500-4500 m/s (3.5-4.5 km/s) for propagation through the Earth's crust and upper mantle). (Earthquake waves travel approximately 2000-4000 times as fast as the Walking and Running students [or approximately 4000-10,000 times as fast as the Slow Walking and Walking students.)
Part Two:
Locating an Earthquake using S
minus P (Walk – Run [or Slow Walk – Run]) times and Triangulation
7. Refer students to Data Table 2, where the next data will be recorded.
8. Outside [or in a room], direct the students, who are representing the P and S waves to agree upon an "epicenter" within the area of the field (within a 30 x 30 m square), [or in the room within a 6 x 6 m square area]. (Note to teacher: Be sure to mark this spot, and measure its distance from the timers, or from the edges of the square area, before leaving the field, so that your students will be able to check their accuracy later.) Station three student timers at different positions around the perimeter of the field to represent seismograph stations. Mark the locations of the stations with flags [or masking tape]. A suggested layout for the seismograph stations is illustrated in Figure 2. The stations are not required to be at the corners of the square area but this geometry is easy and effective and thus enhances understanding of the triangulation method. This diagram can also be used for plotting the segments of circles to locate the epicenter by triangulation.
9. Have the six students representing P and S waves stand at the epicenter (one P wave and one S wave student facing each of the three stations). At the signal, "go," all six of the students representing the seismic waves are to depart from the chosen "epicenter" toward their respective assigned timers ("seismograph stations"), at the speeds that were established in Part One. These students represent the P and S waves that propagate in all directions away from the earthquake focus. By assigning two students to travel to each of the stations, we are representing the P and S propagation paths from the earthquake to the station. (Note to teacher: Pair a student representing an S wave (Walking [or Slow Walking]) with a student representing a P wave (Running [or Walking]); obtaining 3 pairs of simulated earthquake waves traveling in 3 different directions.) Observing the pairs of students representing P and S waves traveling from the epicenter to the stations is a very effective visualization of wave propagation and the meaning of the S minus P times used in the earthquake location method using triangulation.
The timers will measure the length of time BETWEEN the arrival of the Running [or Walking] student ("P- wave") and that of the Walking [or Slow Walking] student ("S- wave"). (On the stopwatch, press start at the arrival of the Running [Walking] student, and press stop at the arrival of the Walking [Slow Walking] student.)
These observations are exactly analogous to
the arrival times of S and P waves. The
time of the earthquake (origin time) is unknown. All that can be determined from the
recordings at a single station is the difference between the P wave arrival
time and the S wave arrival time. (The absolute times of the P and S arrivals
are also known, but the difference between these times is the quantity that is
used for triangulation to locate the epicenter.) This time difference is called the S minus P
(S – P) time and is like the Walk – Run [or Slow Walk – Walk] time of our simulation.
Record this difference, in seconds, on Data Table 2. Repeat this step, and record the difference in arrival times. Recover all materials and return to the classroom.
10. Refer to Data Table 2. Have students use the graph they constructed earlier to determine the distance to the epicenter from each of the seismograph stations. (Use the Walk minus Run [or Slow Walk minus Walk] line to correlate the difference in arrival times to the distance in meters by locating each travel difference on the y axis (time axis) and tracing a line horizontally to the Walk minus Run [Slow Walk minus Walk] line. From this point, trace a line vertically to the x axis (distance axis). The location on the x axis will be the inferred distance from the corresponding station to the epicenter.) An example of these calculations for the sample data is shown in Figure 5. For example, for the sample Slow Walk minus Walk time for station 1 (Column 1, Table 2, Figure 4), locate 8s on the time axis of the travel time curves (Figure 5) and draw a horizontal line to the Slow Walk minus Walk travel time line. From this point, draw a vertical line to the distance axis. The resulting number on the distance axis (5.8m for the station 1 sample data, Figure 4), is the distance that corresponds to a Slow Walk-Walk time of 8s. Enter the distances in Data Table 2.
11. Construct a "map" of the field [or room] on graph paper (Figure 2) with the positions of the stations (timers) marked. Be sure to establish an appropriate scale for your own activity so that it fits on the graph paper (the attached map with stations, Figure 2, could be used for this step; the scales are given for the 30 x 30 m area for the Walk – Run method and for the 6 x 6 m area for the Slow Walk – Walk method using a square geometry for the seismograph station locations). Now the students will use a compass to draw a circle around each timer position (station). The point of the compass should be on the station, and the radius of the circle will be the distance to the epicenter determined in step 10. The point at which the three circles intersect represents the epicenter (see example of triangulation in Figure 3 and the triangulation using the sample data in Figure 6). Because of possible errors in the travel time and distance measurements, the circles may not intersect exactly at one point. Compare the actual location of the epicenter (from distance measurements made in step 8) with the inferred location determined by the triangulation (plot the actual location on the graph). The actual location should be plotted on the graph after the triangulation measurements have been plotted and the estimated epicenter location determined. In this way, the students will be able to compare the location that they found from triangulation with the actual location. Measure the distance on the graph from the actual location to the location determined by triangulation. Check results with teacher. It does not matter if it is not perfect; it is a demonstration of HOW triangulation works. Additional information about earthquakes and earthquake location using the S minus P time method can be found in Bolt (1993, 1999). An interactive earthquake location program using the same method and actual earthquake data (seismograms) is available on the Internet at the Virtual Earthquake web page.
Questions for students after they draw their maps:
1. In what ways were the Walking [Slow Walking] and Running [Walking] students SIMILAR to P and S waves? In what ways were they DIFFERENT?
2. What is the size of the error in the determination of the epicenter by triangulation? How large is the error compared to the distances from the stations to the actual epicenter (the distances traveled by the seismic waves)? What are the possible causes of the error?
3. What were some shortcomings in this activity that prevented us from determining the epicenter perfectly? Do you think these problems could be controlled? Do you have suggestions for how we could improve the experimental design?
Challenge Questions:
4. If the actual arrival time of the P- wave at station number 1 was 10 hours and 0 minutes local time, what was the origin time of the earthquake?
5. The travel-time curves for the Walk – Run [Slow Walk – Walk] times (Figure 1) are approximately straight lines because the Walkers [Slow Walkers] and Runners [Walkers] have approximately constant pace. For seismic waves in the Earth, the travel-time curves for P- and S- waves are curved. What can you infer from this observation?
6. The Epicenter is the point on the surface of the Earth above the focus (hypocenter) of the Earthquake. What effects would a non-zero depth of the earthquake have on our simulation and the travel times of P- and S- waves?
7. If the epicenter of the simulated earthquake was located “outside of the array of timers” (outside of the square area shown in Figure 2), would the earthquake still be able to be located by triangulation? How would the accuracy of the triangulation location be affected by the earthquake being located outside of the array of seismographs? (Try constructing some circular arcs around the stations that correspond to epicenter locations relatively far from all stations.)
References:
Bolt, B.A., Earthquakes and Geological Discovery,
Scientific American Library, W.H.
Bolt, B.A., Earthquakes,
(4th edition), W.H. Freeman & Co.,
Virtual Earthquake, http://vcourseware3.calstatela.edu/.


Figure 1. Travel time graph template for plotting the time of travel for Walk [or Slow Walk] and Run [or Walk] times at three different distances (in addition to the zero distance). The graph is labeled for the Walk – Run method (30 m distance) and for the Slow Walk – Walk method (in brackets [ ], 6 m distance). Plot the times from Data Table 1 using colored pencils or the symbols indicated in the legend in the upper left hand corner of the graph. Draw a line through each of the data sets by connecting the points. Because the speeds of the Walkers [Slow Walkers] and Runners [Walkers] should be approximately constant, the lines should be approximately straight lines.

Figure 2. Graph (map view) of station (timer) locations in a 30 x 30 meter area [6 x 6 meter for the Slow Walk – Walk method]. For convenience, the stations are located at the corners of the square. Scales are provided for the Walk – Run and the Slow Walk – Walk (in brackets) methods. Use the graph to plot circular arcs corresponding to the inferred epicenter to station distances from Data Table 2 and to plot the actual location of the simulated earthquake (epicenter).
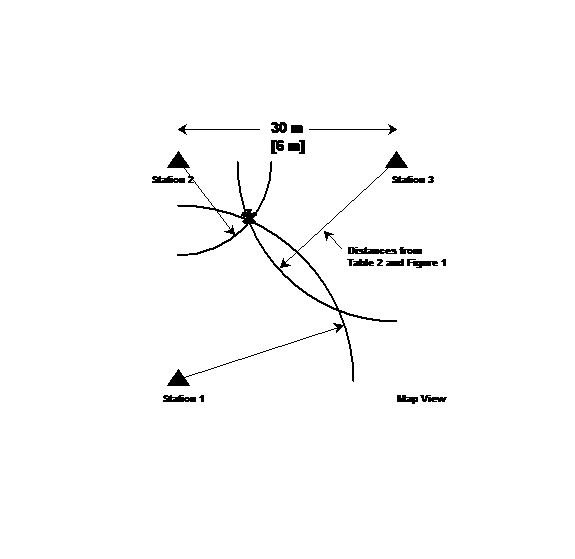
Figure 3. Example of a completed triangulation graph for the Walk – Run method. Circular arcs show the inferred distances (from the Walk minus Run times) from each station (timer). The arcs intersect approximately at a point which is the calculated location. The actual location (asterisk) is close to the location determined by the travel time differences and triangulation.
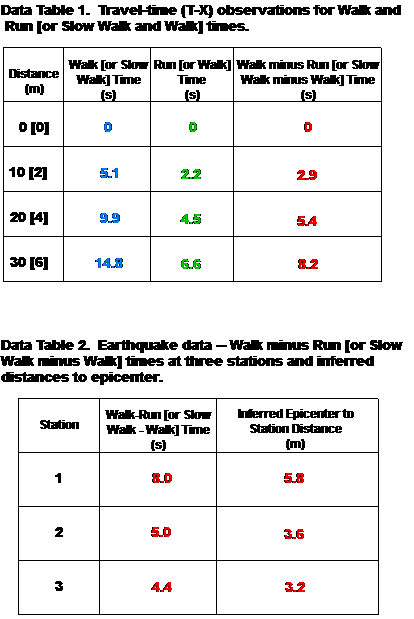
Figure 4. Data Tables 1 and 2 with sample data for the Slow Walk – Walk Method.
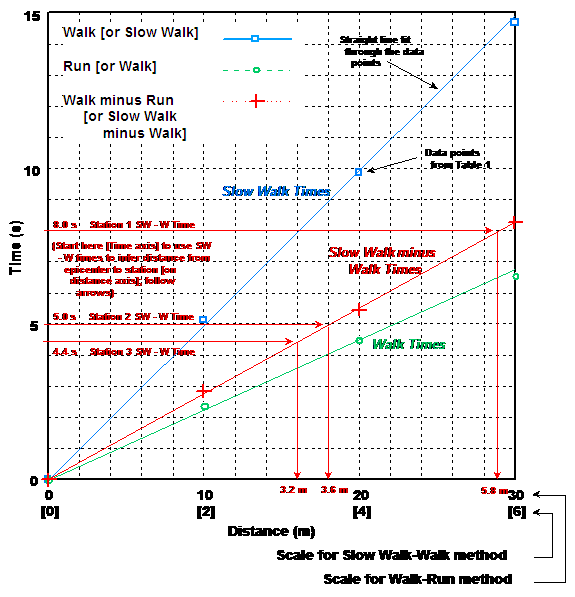
Figure 5. Graph of travel times (travel-time curves) for the Slow Walk, Walk and Slow Walk minus Walk times for the sample data (Figure 4). Note that the data points define nearly straight lines which are drawn through the arrival time data. The points don't fall exactly on the line because of experimental error. For Part Two, measuring the travel times from an epicenter to stations and finding the location of the epicenter by triangulation, the thin horizontal and vertical lines illustrate how to determine the epicenter to station distance from the Slow Walk minus Walk times (S-P times).
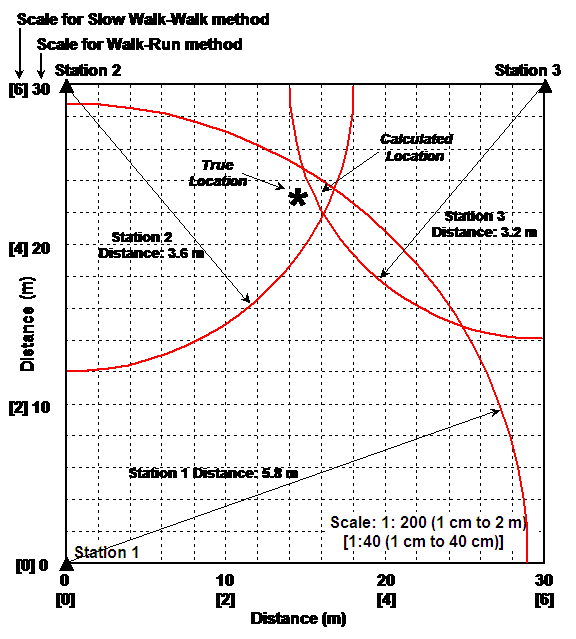
Figure 6. Example of triangulation to calculate the epicenter location from the Slow Walk minus Walk times for the sample data (Figures 4 and 5). Note that because of experimental error, the circular arcs do not exactly intersect. There is also a small difference between the actual and the calculated epicenter location.