EAS 657
Geophysical Inverse Theory
Robert L. Nowack
Lecture 10A
Recursive Least Squares, Kalman Filtering
and Data Assimilation
††††††††††† We will
first consider recursive least squares or Bayesian problem (from Strang,
1986).† Consider the linear problem given
an initial data set d0
with data errors represented by the data covariance matrix ![]() .† If the model
parameters are represented by x, then
.† If the model
parameters are represented by x, then
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (1)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (1)
Assuming no prior, the weighted least square solution can be written
†††††††††††††††††††††††††††††††††††††††††††††††††††††† ![]() †††††††††††††††††††††††††††††††††††††††††††††††††† (2)
†††††††††††††††††††††††††††††††††††††††††††††††††† (2)
and the error in the model parameters as represented by the model covariance matrix
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (3)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (3)
††††††††††† Now assume
new data d1 with ![]() †have arrived.† In order to estimate x using all the data, we have two choices.† The first is to solve the combined problem
which involves reinverting the old data as well, where
†have arrived.† In order to estimate x using all the data, we have two choices.† The first is to solve the combined problem
which involves reinverting the old data as well, where
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† 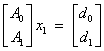 †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (4)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (4)
However, this can be expanded in such a way that the old data has been encoded into x0 and then we solve for x1 using only d1 and x0.
††††††††††† First solve (4) as in (2) assuming that the old and new data are independent where
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† 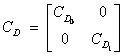
then
††††††††††††††††††††††††††††††††††††††††††††††††††  ††††††††††††††††††††††††††††††††††††††††††††† (5)
††††††††††††††††††††††††††††††††††††††††††††† (5)
and
†††††††††††††††††††††††††††††††††††††††††††††††††††††† ![]()
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ![]() †††††††††††††††††††††††††††††††††††††††††††††††††††† (5a)
†††††††††††††††††††††††††††††††††††††††††††††††††††† (5a)
The solution for x1 is then
††††††††††††††††††††††††††††††††††††††††††††††††††† ![]()
††††††††††††††††††††††††††††††††††††††††††††††††††††† ![]()
††††††††††††††††††††††††††††††††††††††††† ![]()
However, this can be written as
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (5b)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (5b)
which is called the gain matrix and
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ![]() ††††††††††††††††††††††††††††††††††††††††††††††††††† (5c)
††††††††††††††††††††††††††††††††††††††††††††††††††† (5c)
where ![]() †is called the
prediction error or the innovation.†† In
this case, the old data does not need to be reinverted, rather
†is called the
prediction error or the innovation.†† In
this case, the old data does not need to be reinverted, rather ![]() †are updated from
†are updated from ![]() †given only the new data
†given only the new data ![]() .† One could envision a
situation where an initial experiment was done, say
from a seismic tomography experiment, giving a result
.† One could envision a
situation where an initial experiment was done, say
from a seismic tomography experiment, giving a result ![]() †and then a few years
later a new experiment is done by other researchers.† However, the new researchers donít have
access to the old data, but only the earlier results.† Nonetheless, they can still incorporate the
old data which has been encoded into the earlier model result.
†and then a few years
later a new experiment is done by other researchers.† However, the new researchers donít have
access to the old data, but only the earlier results.† Nonetheless, they can still incorporate the
old data which has been encoded into the earlier model result.
††††††††††† From a Bayesian perspective, the earlier model and its uncertainty acts as a prior for the new experiment and recursive least squares gives an operational interpretation.† This can also be considered a recursive Bayesian inversion.
††††††††††† For many types of experiments with data regularly coming in over time, this can be generalized to a continually updating process as
††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††† (6)
††††††††††††††††††††††††††††††††††††††††††††††††††††† (6)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (6a)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (6a)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††† ![]() ††††††††††††††††††††††††††††††††††††††††††††††††† (6b)
††††††††††††††††††††††††††††††††††††††††††††††††† (6b)
In this case, the subscript i would also imply a progression in time.†
For these cases with new data arriving in time, one could estimate the parameters of the model or the state of the system at the next time by some basic physics which could be incorporated into the estimation process to stabilize the results.† This would imply some kind of averaging between a prediction based on the physics and an estimate from measurements that could be noisy for the state of the system at the next instance in time.
††††††††††† As an example, consider determining the position of a car.† If a car is equipped with a GPS unit, then at each time a measurement of the position can be made.† However, the GPS estimates are likely to be noisy and jump around with errors of a few meters.† The carís position can also be estimated by knowing the speed and direction that the car is moving from an earlier position.† Typically, this will give a smoother estimate of the carís position.† However, this estimate is likely to drift over time based on uncertainties in the carís speed.† Thus, combining the estimate of the cars location from incoming, but noisy, measurements and estimates based on the physics of the moving car will likely give a more robust estimate.
††††††††††† This is the strategy in Kalman filtering which works recursively to calculate the new state of the system.† It has had early applications for trajectory estimation in the Apollo program and now is used regularly for navigation guidance systems (i.e., for missile systems).
††††††††††† Kalman filtering include a measurement update step and a predictor step:
1)†† Measurements d0,d1,Ödm
up to time, ![]() , where di
= Aixi
, where di
= Aixi
2)†† A physical law or model governing the change in the state as time goes forward
†††††††††††††††††††††††††††††††††††††††† ![]() ††††† with a different Fi
at each step
††††† with a different Fi
at each step
This is then solved iteratively as
†††††††††††††††††††††††††††††† †††††††† ![]() †††††(with errors ei
as incorporated into
†††††(with errors ei
as incorporated into ![]() )
)
††††††††††††††††††††††††††††††††††††† ![]() †††† (with a modeling uncertainty ei)
†††† (with a modeling uncertainty ei)
This can be combined as
††††††††††††††††††††††††††††††††††††††††††††† 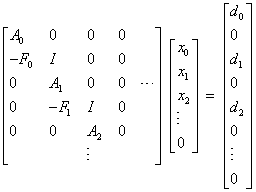
For recursive least squares or Bayesian inversion, xi+1 = xi and Fi = I.
††††††††††† There are many different flavors of Kalman filtering.† The extended Kalman filter allows for nonlinear transition functions which are then linearized.† In ensemble Kalman filtering, the covariance matrices are approximated by sample covariances via a Monte-Carlo implementation.
††††††††††† Data assimilation arises in many fields of the geosciences, including numerical weather forecasting and prediction (NWP) and hydrological applications.†
For NWP, at each time step observations of the current (and possibly past) state are combined with the results of a numerical weather prediction code (the forecast) to produce an analysis of the best estimate of the state of the system.† An important limitation for NWP is that the physical models are highly nonlinear often leading to a high sensitivity to initial conditions and a breakdown in predictive ability.† Thus, a weather forecaster can often tell you what tomorrowís weather is, but not three months in the future.
The aim of data assimilation is to simulate the weather combining satellite and ground based measurements at specific and discrete times and locations with a numerical weather forecasting model which predicts atmospheric variables at every grid position and time step in order to track the real atmosphere.
More information on Kalman filtering and approximations and specializations to meterological data assimilation analysis and NWP can be found in:
Rodgers, C.D. (2000)† Inverse Methods for Atmospheric Sounding, World Scientific.
Kalnay, E. (2006)† Atmospheric Modeling, Data Assimilation and Predictability, Cambridge Press.
Kalmon filtering for general geophysical fluid applications is presented by:
Wunsch, K. (2006)† Discrete Inverse and State Estimation Problems, Cambridge Press.