EAS 657
Geophysical Inverse Theory
Robert L. Nowack
Lecture 2
Several Inverse
Problems in Geophysics
Several historical examples of inverse problems are now given.
18th century
Gauss developed
the method of least squares and applied it to a number of problems including
geodetic mapping, estimation of orbital parameters of the asteroid Ceres, and
problems in magnetism. However, the
first published description of least squares was given by Legendre.
19th century
The estimation of the age of the Earth has been an important problem in the earth sciences. Lord Kelvin gave several estimates of the age of the Earth from 20 to 100 million years. These estimates were based on the premise that the Earth’s outward heat flow represents cooling of an initially molten body. But, these estimates were done with inaccurate estimates of the thermal conductivity structure of the Earth. In addition, there was the unknown physics of radioactivity when these estimates were made. With the addition of heat sources due to radioactive decay and the use of radioactive age dating, a current estimate of the age of the Earth as 4,560 million years.
19th-20th century
The figure and shape of the Earth has been another important problem in the earth sciences. But the early scientists had only inadequate data. With satellite data, the Earth is now known to have an equatorial bulge of about 20 km and is slightly pear-shaped.
Since the development of the seismograph, seismic travel time data have been used to invert for the structure of the Earth’s interior. Scientists doing early work on Earth structure were Herlglotz, Wiechert, Jeffreys, Bullen, and Gutenberg. Inge Lehmann, a Danish seismologist, discovered the Earth’s inner core in 1936 using seismic waves. Early studies emphasized radial earth structure. Recent inversions of seismic data have inferred 3-D models of the Earth’s interior. Iterative inversion methods have been used to perform tomographic inversions as wellas to study the resolving power and uniqueness of the solutions.
Prediction of Dynamical Systems
Prediction of dynamical systems requires a detailed understanding of these systems. It also requires knowledge of the loss of information by systems themself. Examples include:
Weather prediction – The weather system is highly nonlinear with many variables and can be chaotic. Long term weather predictions may be theoretically impossible.
Earthquake
prediction – Historical seismicity catalogs and other geophysical data are used
to try to predict future earthquakes.
The system is also highly nonlinear with many variables. In 1975, the Chinese successfully predicted
the Haicheng earthquake. But in 1976,
they did not predict at all the
Predictive deconvolution – For this problem, prediction error filtering is done on reflection seismic data to separate the large predictable ocean bottom multiples from the unpredictable echoes from geologic structures at greater depths. After its development in the 1950’s and 1960’s, it allowed for offshore oil exploration to be done.
Construction of Discrete Linearized Inverse
Problems
I will now give a brief overview of discrete and linearized inverse problems.
Consider a discrete set of model parameters mj, i.e., density in “chunks” of the Earth.
A particular model will predict
certain data. Let 
be the observed data
and 
be the predicted data
given some model, mj, thus
.
We want to find the model parameters
that will give the predicted data as close as possible to the actual
observations. We will begin by expanding
fi(mj) as a
formal 
(i.e., a homogeneous
Earth model, for example). Thus,
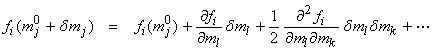
where 
is a small change to
the jth model parameter. Note repeated
indices in a particular term imply a sum on that index. Now,
and
.
Using just the
first two terms in the
.
This linearized
equation can then be iterated to obtain improved estimates of the model
parameters mj. The first estimate would be 
for all indices j of the model. For the case of discrete data and model
parameters, this linearized equation results in a linear matrix equation
where now di is some data residual
vector and is a model residual
vector to be solved for, and Gij
is the sensitivity operator of the data to the model. A great deal of effort will be expended in order
to understand linear systems and discretized matrix equations.
Matrix analysis is a discretized analog of linear systems. Continuous operators can be approximated by matrix operators and matrix analysis is often a practical way of obtaining numerical results or for studying the basic properties of the operators.
Ex) Consider a linear integral equation (Fredholm equation of 1st kind)
where d(y) is given, k(y,x) is the kernel of the integral, and we want to find m(x). Using numerical integration, then
.
For a given d(yi), i = 1,M, then
.
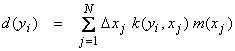Now let
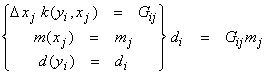
where
N columns
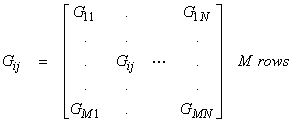
This is a M (rows) x N (columns) matrix. We will also write this as d = Gm.
We have thus succeeded in replacing an integral equation by a matrix equation whose solution gives us an approximate numerical evaluation of the integral equation for m(x).
Ex) Differential equations can also be approximated using matrices. For example, consider the differential equation
To numerically approximate this equation, use a second order difference,
where 
is a forward
difference and 
is a backward
difference. Then,
where 
and 
.
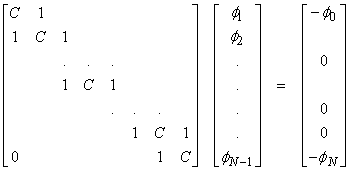
This is a linear system of equations. It can be written as a tridiagonal matrix system, but we must also provide boundary conditions.
1) 
at the endpoints in x are given. For k
= constant, then let
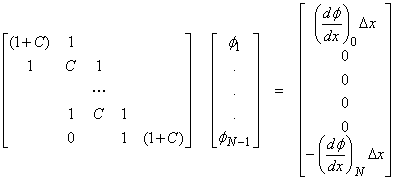
2) 
at the endpoints in x are given. Let
Matrix Manipulations
Given that integral and differential equations can often be approximated by matrix equations, several matrix operations are given below. Both matrix and index notation are given.
Addition
A + B + C ; Aij + Bij = Cij
Multiplication
AB = C
; 
Note: the column length of A must equal the row length of B for this to be defined.
In general, AB 
BA. Thus, matrices multiplication doesn’t, in
general, commute and may not even be defined.
Transposition
AT = B ; Bij = Aji
Complex conjugate transposition
A* = B
; Bij = 
Note:
(AB)*
= B*A*
A single column matrix is called a vector (or column vector). A single row matrix is called a row vector.
From this very brief review of matrices, we will turn to abstract vector spaces and define Banach and Hilbert spaces.