Purdue University

EAS 657

Geophysical Inverse Theory

Robert L. Nowack

Lecture 3

Linear Vector Spaces and Subspaces

In this section, a brief review is given of linear vector spaces.

A vector space V is defined by

a) A collection of elements called “vectors”.

b) A field of scalars, F.

A linear vector space has the following properties

vector addition:

closure: if v₁, v₂, V, then v₁ + v₂ V

commutative: v₁ + v_{2 =} v₂ + v₁

unique zero: 0 such that if v V, then v + 0 = v

unique inverse: -v such that if v V, then v + (-v) = 0

scalar multiplication: v

closure if v V, F, then v V

linearity: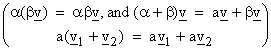

Ex) n-tuples

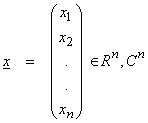
Rⁿ = real elements or Cⁿ = complex elements

Ex) An infinite sequence of real numbers. We will be interested in bounded sequences for which {x_k} < M for all k where M is some constant.

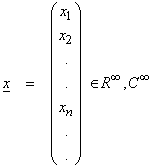
Ex) Consider the interval C[a,b] on the real line. The collection of all continuous real valued functions f(t) on this interval is a linear vector space. The zero vector is the function identically zero on [a,b].

Ex) The collection of polynomial functions on the interval [a,b] is a linear vector space.

Subspaces: The subspace V₁ of V contains a subset of V and is also a vector space.

Ex)

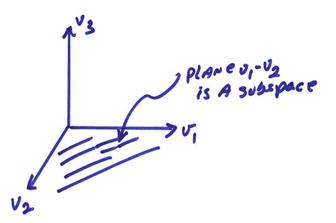
The plane v₁-v₂ is a subspace

Ex)

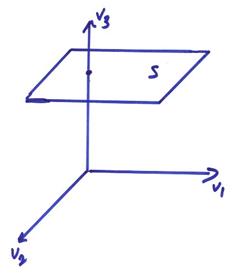
Is S a subspace? No, it doesn’t include the zero vector! But

S = V¢ +

The space S is nonetheless very important and is called a hyperplane.

Ex)

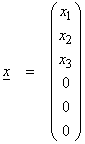
is a subspace of Rⁿ.

Def: A set of vectors v₁, … v_N V are linearly dependent iff (if and only if) there exists a set of scalars, , not all zero, such that

Otherwise the set of vectors are called linearly independent.

Ex)

2 v₁ + 1 v₂ = 0

Thus, these 2 vectors are linearly dependent.

Ex)

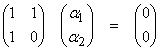
This equation only has the trivial solution

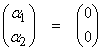
Thus v₁ and v₂ are linearly independent.

Ex) The function space C[a,b] of continuous functions on [a,b].

In the figure below, the functions on the left are linearly dependent and the functions on the right are linearly independent.

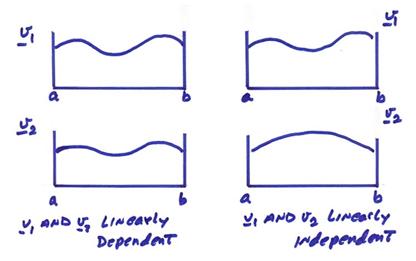
A vector v can be written in terms of v₁ … v_N if there exists scalars, , such that

A set of vectors spans a subspace if all the vectors in can be expressed in terms of this set of vectors.

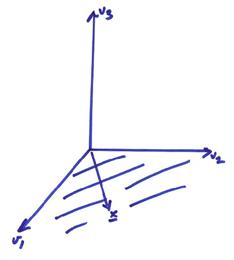
Ex) In the figure below, vectors v₁,v₂ span the v₁ - v₂ plane, but v₁,x also span the n₁ - n₂ plane.

A Basis is a linearly independent set of vectors which span the vector space.

Ex) The standard basis for R^N is

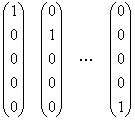
Note that this basis is not unique. However, every basis for a given vector space has the same number of vectors.

Theorem: Every basis of a given vector space have the number of basis vectors or dimension.

Theorem: A vector space having a finite basis is said to be finite dimensional. All other vector spaces are said to be infinite dimensional.

Theorem: Given a basis v₁, … v_N for a vector space v, if , then .

Proof:

But because v_i are independent, then .

If u₁, …, u_k are linearly independent vectors for k < N where N is the dimension of the vector space, we can always construct a basis by adding additional independent vectors.

u₁, …, u_k, u_k+1, …, u_N

A vector space can be decomposed into independent subspaces instead of vectors. Thus,

V = V₁ + V₂ + V₃ … V_m

This is called a direct sum decomposition. It is like a basis decomposition when V_i all have dimension 1. For a basis v₁,v₂ … v_N, then

V = v₁ + v₂ + … + v_N

Ex) In the figure below, the vector space v can be written as a direct sum decomposition as

V = v₁ + v₂ + v₃

or

V = V₁ + v₃

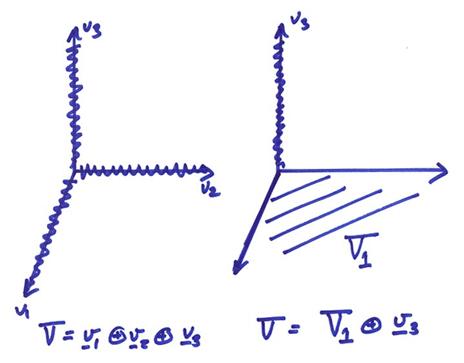
If V = U + W, then Dim V = Dim U + Dim V where U W = {0}.

The Concept of Length

A vector space with a defined measure of length is called a Normed Vector Space. This adds a great deal more structure to a vector space. A normed vector space has a defined mapping from V R¹ noted as || v || satisfying

1) || v || > 0 for all v V || v || = 0 only if v = 0

2) || v || = | | || v ||

3) || v₁ + v₂ || < || v₁ || + || v₂ ||

The length measure can also be used to measure the “Distance” between two vectors. For V = R^N, then different length measures or norms are possible.

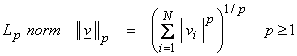
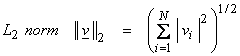
Ex) V = C [a,b]

The distance between two vectors can be written in terms of the norm as

d = || x - y ||_p

For finite dimensional spaces there exist C₁,C₂, such that

C₁ || v ||_A < || v ||_B < C₂ || v ||_A

From this, proofs of convergence with one norm can be transferred to other norms.

A complete normed vector space is called a Banach space. A metric space is complete if every Cauchy sequence in the space converges to some point v in the vector space V.

A sequence {v_N} contained in a normed vector space (V,d) is called a Cauchy sequence if for every > 0 there exists an integer such that if , then d(v_m1,v_m2) < .

Ex) The rational numbers are not complete on the real line V = R¹,d(x,y) = | x-y | where a rational number is a set of all fractions of integers equivalent to some fixed fraction, .5 = 1/2 = 2/4 = 6/12 … The rational numbers are incomplete because imbedded within the rationals are the “irrational numbers” which are nonperiodic infinite decimals.

Ex) , are irrational numbers.

Truncated irrationals are a sequence of rationals converging in the limit to the given irrational number.

Real numbers (rational + irrationals) are complete on the real line. (Note, however, that rationals are dense on the real line since “nearby” every irrational number is a corresponding rational number.

The real line (V = R¹, d = || x-y ||_p) forms a Banach space. By extension, V = R^N, d = || x-y ||_p forms a Banach space. Since any finite dimensional vector space can be mapped in a one to one fashion to R^N, then:

Theorem: In a normed linear vector space, any finite-dimensional subspace is complete and hence forms a Banach space.

For an infinite sequence of functions f(t) that are continuous on [0, 1] where and , consider a Cauchy sequence of functions

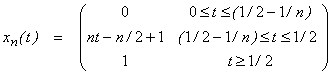
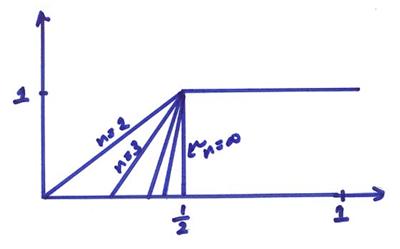
Since the convergence point is not a continuous function, this normed space is not complete and hence is not a Banach space. This space can, however, be made complete by adding certain discontinuous functions. We will then call this L_p[a,b] and this is a Banach space.

The infinite n-tuples

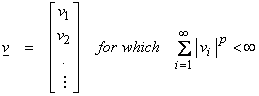
form a Banach space. This is called lp.

Note that care must be taken with infinite dimensional spaces to avoid pathological cases.

Now we need to introduce some concepts of directionality. Recall that the dot product of two physical vectors a and b is

= | a | | b | cos

We can use this to define the “angle” between two vectors, where

The dot product must be defined in such a way that

| | < | a | | b |

We can use this to define orthogonality of two vectors in a vector space. For a general vector space, we will call the inner product (a,b). The inner product maps x,yV into the scalars (real or complex) satisfying (Note: the math notation is: or (a,b) and the physics notation is <a,b> or <a êb>).

1) (x,y) = (y,x)* (* is here just the complex conjugation).

2) (x + y,z) = (x,z) + (y,z).

3) (ax,z) = a(x,z). (properties 2 and 3 define the linearity of the inner product)

3’) (x,az) = a*(x,z).

4) (x,x) > 0 for x 0 and (x,x) = 0 for x = 0.

(V,(x,y)) forms an Inner Product Space.

A suitable norm in an inner product space is:

This is an induced norm from the defined inner product. With this norm, then we can show Schwarz’s inequality

.

Equality holds for x = y or x = 0.

The angle between two vectors is defined as

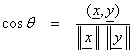
Ex) In R^N, let An induced norm from the inner product is then

.

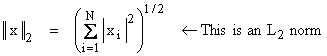We could also define other norms, for example

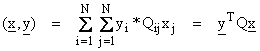
where Q is a positive definite operator such that

x* Q x > 0

for an arbitrary x (where) Q is Hermitian Q* = Q (to be defined a little later on).

Ex) For V = C[a,b], define the inner product to be

or a more general definition is

where

K(t,s) = K*(s,t)

A complete inner product space is called a Hilbert space (recall all finite dimensional spaces are complete by virtue of the completeness of R¹ and hence R^N).

Define two vectors to be orthogonal if (x,y) = 0. = 90° implies that x is perpendicular to y. Note by changing the inner product by a change in Q, we can change the definition of the angles between vectors.

A set of vectors s₁, …, s_k are orthogonal if the vectors are pair-wise orthogonal.

A vector x is said to be orthogonal to a subspace S if x is perpendicular to any y in S.

Subspace S₁ is perpendicular to S₂ if x is perpendicular to y where x S₁ and y S₂. Let S be any subspace in V, then

S^perp = (v V | v is perpendicular to S).

This is called the orthogonal complement of S.