Purdue University
EAS 657
Geophysical Inverse Theory
Robert L. Nowack
Lecture 3a
Vectors in Hilbert
Space
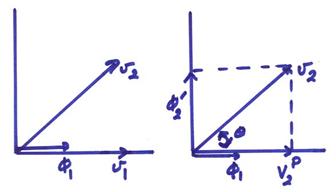
Given a basis for V, (v1,…vN) and a defined
inner product, the Gram Schmidt
procedure can be used to construct an orthonormal basis (![]() ,…
,… ![]() ).
).
a) Let
![]()
b) Find
the “orthogonal projection” of v2
on ![]() (drop a
perpendicular), then subtract this part from v2. The
angle between
(drop a
perpendicular), then subtract this part from v2. The
angle between ![]() and v2 is obtained from
the inner product as
and v2 is obtained from
the inner product as
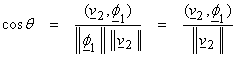
Now, ![]() should be parallel to
should be parallel to ![]() , where
, where
![]()
This gives
![]()
Then,
![]()
and
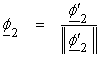
If this procedure is continued, then
![]()
and
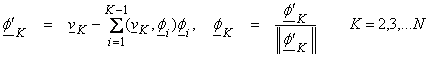
CONVERSE: Given a basis v1,…vN of a vector space V, one can always find an inner product such that v1,…vN are orthonormal. This can be done by modifying the definition of the inner product.
(x,y) = yTQx
Choose Q such that x,y are orthonormal.
If ![]() , i=1,N are orthonormal, then
, i=1,N are orthonormal, then
![]()
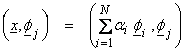 for j = 1,…,N
for j = 1,…,N
![]()
since for an orthonormal basis,
(![]() ,
,![]() ) =
) = ![]()
then,
![]()
The representation of a vector
using an orthonormal basis is called a Generalized
Fourier Series, where
![]()
with an inner product such that
![]() are orthonormal. Note that care must be taken for infinite
dimensional spaces.
are orthonormal. Note that care must be taken for infinite
dimensional spaces.
Now let’s investigate Signal Spaces L2[a,b]. This is the space of square-integrable functions on the line [a,b]. Thus,
![]()
This is an infinite dimensional space with inner product defined as
![]()
and an induced norm
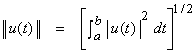
Ex) For the set of all periodic signals with period T on L2[0,T], choose the complex exponentials
![]()
where
![]() and k
=
and k
= ![]() , … -1, 0, 1, …
, … -1, 0, 1, … ![]()
The ![]() are orthogonal since
are orthogonal since
![]()
![]()
Let
![]()
![]()
then,
![]()
Thus ![]() are orthogonal on L2[0,T]. Let,
are orthogonal on L2[0,T]. Let,
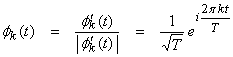 k = -¥,
…-1,0, + 1,…¥
k = -¥,
…-1,0, + 1,…¥
See Luenberger (1968) p. 61-62. These are orthonormal and can also be shown to be complete in L2[0,T]. Now any function in L2[0,T] can be expressed as
![]()
where
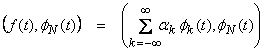
![]()
and
![]()
This is called a Generalized Fourier Series since we are free to choose any orthonormal basis. For
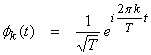
then,
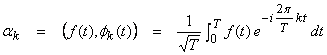
The ![]() are the Fourier
coefficients called the Discrete
spectrum of f(t).
are the Fourier
coefficients called the Discrete
spectrum of f(t).
A Fourier series pair for L2[0,T] can be written

where ![]() .
.
If we look at the unbounded interval
[-![]() , +
, +![]() ], the functions
], the functions ![]() are not
square-integrable. But if we relax this
requirement and look at basis functions
are not
square-integrable. But if we relax this
requirement and look at basis functions ![]() , then
, then
![]() .
.
![]() is a generalized
function called a Delta function, where
is a generalized
function called a Delta function, where
![]()
and
![]()
Then,
![]()
where
![]()
![]()
![]()
Thus,
![]()
or
![]()
The spectrum has now coalesced into
a continuous function, ![]() . Thus, the Continuous Fourier transform pair on
. Thus, the Continuous Fourier transform pair on ![]() with the assistance of
generalized functions (a relaxation of the square integrable condition) can be
written
with the assistance of
generalized functions (a relaxation of the square integrable condition) can be
written
![]()
![]()
However, we aren’t limited to complex exponentials!
Ex) Consider
discrete signals where ![]()

Let the
discrete ![]() function be written
function be written
![]()
then,
![]()
where u[k]
are the coefficients and ![]() are the basis functions.
are the basis functions.
Define the inner product to be,
![]()
Now, is the
basis ![]() orthonormal? Yes, since
orthonormal? Yes, since
![]()
Let
![]()
then,
![]()
![]()
Thus,
![]()
The individual sample points provide one basis for a discrete time series.
Ex) Continuous signals that are bandlimited in
frequency forming a subspace of ![]()
The sampling theorem states that one can completely reconstruct a continuous bandlimited signal from a discrete sampling of the signal. This can be written as
![]()
where ![]() are the discrete
samples with a sampling period T. This
is exact if the highest frequency in the signal is less than
are the discrete
samples with a sampling period T. This
is exact if the highest frequency in the signal is less than ![]() .
.
The “impulse response” of this
system is 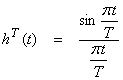 where
where ![]() is a sinc
function.
is a sinc
function.
In terms of a generalized Fourier
series, then the basis functions are ![]() with inner product
with inner product ![]() .
.
Since ![]() , then the basis is orthonormal. The coefficient
, then the basis is orthonormal. The coefficient ![]() can be written
can be written
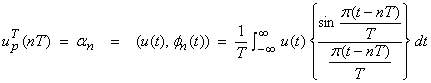
Polynomials
The polynomials tk are independent, but not orthogonal on L2[-1,1]
![]()
with inner
product ![]() on the interval [-1, 1].
on the interval [-1, 1].
We can use Gram Schmidt to find an orthonormal basis, then,
![]()
where Pk(t) are called Legendre polynomials with
![]()
The problem with the polynomials, tk, is that they are not nearly orthogonal and an orthonormal basis is preferred. Using different inner products, then different orthogonal polynomials can be obtained.
Ex) Modify the inner product on L2[-1,1]. Choose
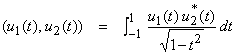
Using Gram Schmidt results in the Chebychev polynomials
![]()
where
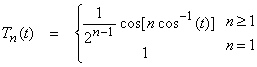
The first several Chebychev polynomials are,
![]()
Parseval’s Theorem
Assume two orthonormal bases for the
same vector space V, say ![]() and
and ![]() with a specified inner
product. Given two vectors, v1, v2, then
with a specified inner
product. Given two vectors, v1, v2, then
![]()
This is called the generalized Parseval’s theorem. Note that the ordinary Parseval’s theorem states that power is conserved, or
Power in the time domain = Power in the frequency domain.
Let
![]() and
and ![]()
Then,
![]()
This results
since the ![]() are orthonormal, thus
are orthonormal, thus
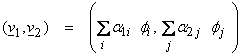
![]()
Now use another basis with same inner product, then
![]() and
and ![]()
and
![]()
Now the value of the inner product should be preserved regardless of the basis, then
![]()
This is the generalized Parseval’s Theorem.
Ex) Assume an inner product
![]()
Use a basis ![]() where
where ![]() , then the coefficient are the Fourier series.
, then the coefficient are the Fourier series.
![]() and
and ![]()
Then,
![]()
For ![]() , then
, then
![]()
Thus, the squared sum in one period equals the sum of squared Fourier coefficients.