| |
|
Meredith's rule D of Condensed Detachment
TERMINOLOGICAL PRELIMINARIES
Pick any sentential language, L,
that includes a binary connective, say C, and let the rules of
detachment/modus ponens (for C) and of (uniform)
substitution be formulated as usual.
Where Cαβ
and
γ are any pair
of formulas, let
γ' be an alphabetic variant
of
γ containing no
letters occurring in Cαβ.
If there exists a substitution
σ
of formulas for the letters occurring in
a and
γ' for which
σ(α)
=
σ(γ'),
then
α and
γ' are said to be unifiable, and
σ is called a unifier
for them. When α and
γ' are unifiable, there is, by the Unification
Theorem of J. A. Robinson's A machine-oriented logic based on the
resolution principle, [Journal of the Association for Computing
Machinery, volume 12 (1965), pp. 23-41], always a most general
unifier for the two, that is, a substitution
σ of formulas for the
letters occurring in α and
γ' such that for any other substitution
σ' unifying
α and
γ',
σ'(α)
is a substitution instance of
σ(α).
By trivial letter-for-letter alterations,
σ can always be turned into a
β-acceptable most
general unifier
σ*
for α and
γ', that is, a most
general unifier for α and
γ' for which no sentence letters occurring in
σ*(α)
occur in β but not
α. Our rule can now be
formulated as follows:
FORMULATION OF THE
RULE D
OF CONDENSED DETACHMENT
Premises: Any two formulas Cαβ
(the major premise) and
γ
(the minor premise) for which
α
and
γ have a common
substitution instance.
Conclusion:
any alphabetic variant of
σ*(β)
where
γ' is any
alphabetic variant of
γ containing no sentence letters in common with Cαβ,
and
σ* is any
β-acceptable most general unifier for
α and
γ'.
THE CRUCIAL
METATHEOREM
The basic result
[the first published proof I'm aware of is in J. A. Kalman's
Condensed detachment as a rule of inference, Studia Logica,
volume 42 (1983), pp. 443-451, though the result was certainly known to
Meredith, Prior, and many others, and had presumably been proved by them
earlier though not published] is this:
METATHEOREM.
For each set A of wffs of L, let the formulas classically derivable
from those in A be the formulas that can be derived from those in A using
the rules of Detachment and Uniform Substitution, and let the formulas
D-derivable from those in A be the formulas that can be derived from
those in A using the rule D of Condensed Detachment alone. Then a
formula is classically derivable from formulas in A if and only if it is a
substitution instance of at least one formula D-derivable from formulas in
A.
AN EXAMPLE PROOF USING CONDENSED DETACHMENT
To illustrate the use of condensed detachment and, as
well, the way proofs are presented on these pages, here is a simple
derivation of the two formulas CpCCpqq and CCCppqq
(nicknamed "Pon" and "Specialized Assertion", respectively)
from the two formulas CCpCqrCqCpr ("Com", or just "C")
and Cpp ("Id") using rule D:
1.
CCpCqrCqCpr
2.
Cpp
D1.2 = 3.
CpCCpqq
D3.2 = 4.
CCCppqq
The annotation "D1.2" to the left of line 3
tells us that line 3 is the result of applying rule D using line 1
as major premise and line 2 as minor premise.
When studying a proof of
this sort, one can always work out the substitutions for one's self,
though it's often easier to do so with pencil and paper than in one's
head. Here, notice that we can replace both occurrences of 'p'
in 1 with 'Cpq', both occurrences of 'q'
with 'p', and both occurrences of 'r'
with 'q' to get 'CCCpqCpqCpCCpqq'.
In 2, we can replace both occurrences of 'p'
with 'Cpq' to produce 'CCpqCpq'.
Since the substitution instance of 2 thus obtained matches exactly the
antecedent of the instance of 1 gotten earlier, the result of detaching
the former from the latter (equivalently, "the result of applying
modus ponens with the former as minor premise and the latter as
major") leaves us with the consequent, 'CpCCpqq',
of the longer formula, which is shown in the proof as line 3.
Similarly, the expression
"D3.2" appearing left of line 4 informs us that line 4 is the most general
formula that can be obtained by detaching a substitution instance of line
2 from an instance of line 3. In this case, things are much easier.
Simply replace each 'p' in line 3 with 'Cpp'
to get 'CCppCCCppqq'.
Line 2 is the antecedent of the latter, whence detaching it delivers 'CCCppqq'.
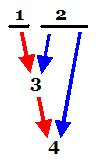
Occasionally it can be
useful to draw a "picture" of the proof in which, for each individual
application of rule D, a red
arrow is extended downwards
from the major premise and a blue
arrow down from the minor premise towards the line produced by that
application:
As a curiosity, I mention that the pair {C, I} used in the
example above can be compressed into the single axiom CCCCpCqrCqCprCCsstt:
C and I follow quickly from it (with it as line 1,
D1.1 = 2 = Specialized Assertion, D2.1 = 3 = Pon,
D2.2 = I, and D1.3 = C), and it in turn
follows from them (though not as easily: four applications of D
are needed). |