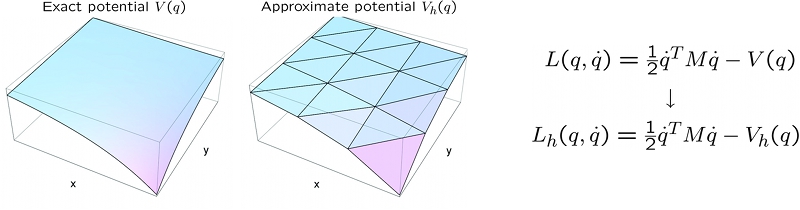
We formulate an integration scheme for Lagrangian mechanics, referred to as the force-stepping scheme, that is symplectic, energy conserving, time-reversible and convergent with automatic selection of the time step size. The scheme also conserves approximately all the momentum maps associated with the symmetries of the system. Exact conservation of momentum maps may additionally be achieved by recourse to Lagrangian reduction. The force-stepping scheme is obtained by replacing the potential energy by a piecewise afine approximation over a simplicial grid, or regular triangulation. By taking triangulations of diminishing size, an approximating sequence of energies is generated. 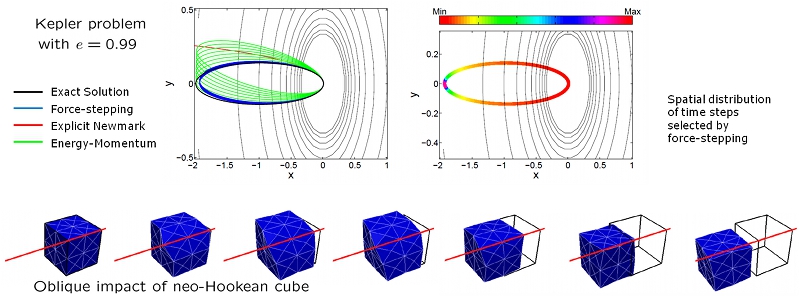The trajectories of the resulting approximate Lagrangians can be characterized explicitly and consist of piecewise parabolic motion, or free fall. Selected numerical tests demonstrate the excellent long-term behavior of force-stepping, its automatic time-step selection property, and the ease with which it deals with constraints, including contact problems.