Purdue University

EAS 557

Introduction to Seismology

Robert L. Nowack

Lecture 5

Now we begin developing some of the basic concepts of continuum mechanics that we will need to study the propagation of elastic waves in the Earth. It is these elastic waves that are recorded on seismographs. The information they contain provides us with much of what we know about both earthquake sources and the structure of the Earth’s interior. So, it is important for us to understand the fundamentals if we are to properly interpret the information brought to us about the Earth’s interior by the elastic wave types we see on seismograms.

The concepts of stress and strain are fundamental to describing the force balance and geometrical description of continuous deformable bodies (like the Earth). The relation between stress and strain allows us to relate the applied forces to the resulting deformation in much the same way that the extension of a spring is related to the force pulling on it.

The particular kind of relation between stress and strain that we shall derive is called linear elasticity because the resulting strain is linearly proportional to the applied stress. So, to a high degree of precision, the Earth can be modeled as a linear elastic system over the short time span of seismic waves and, using observations of elastic waves, we can derive the elastic properties within the Earth.

Analysis of Strain

We shall consider a fixed set of axes and express all vectors and “tensors” in terms of their components with respect to these axes. First, several definitions:

A Deformable body = a body that changes shape under the action of forces (internal (like gravity) or external forces)

A Rigid (nondeformable) body = a body that undergoes only rigid motions (i.e., translations and rotations).

Deformation = strain = the change of relative position of points within the body (distortion stretch, etc.).

The assumptions on a continuum are

1) continuity of deformation (i.e., no tears or dislocations within body)

2) single valued deformation (i.e., 1-1 correspondence in strained and unstrained configuration

Consider a material in which a particle initially having position moves to some other point . We will write

where is the position and time dependent displacement.

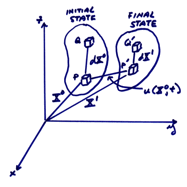
The distance between particles P and Q in the initial state is . After deformation, P is displaced by to and Q is displaced to . Note that we define in terms of [a Lagrangian description - a function of where it comes from], or in terms of [a Eularian description – a function of where the particle is]. For infinitesimal deformation of linear elasticity, it is simpler to use the Lagrangian description.

The separation between the displaced particles and is . This can be written from the figure

(1)

Now we want to express in terms of and . Use a Taylor expansion of

where .

In the vicinity of P at , we can find the changes in length of any elementary line, segment to first order as

where the summation convention over repeated indices can be used to suppress the summation sign. In vector notation,

(2)

where is the outer product,

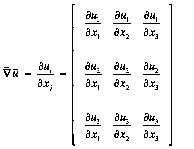
where are the components of the displacement vector in the figure above. This includes 9 partial derivatives and is a rank 2 tensor. A linearized version of equation (1), in component form, can then be written as,

(sum on j) (3)

In order to give a physically meaningful representation of the local deformation, we separate into its symmetric and antisymmetric parts. Thus,

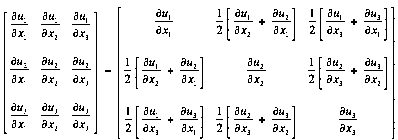
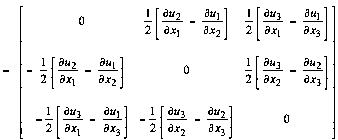
In an abridged notation, let

This is the infinitesimal strain tensor which is symmetric (in the infinitesimal case, there is no distinction between Langrangian and Euclerian descriptions), and

This is the rotation tensor which is antisymmetric.

The above equation can then be written

Thus, the infinitesimal strain tensor has six independent components, and , and the rotation tensor has three independent components, . We will now give a physical interpretation of these components.

The Physical Interpretation of Strain and Rotation

Consider first in 2-D

A) Tensional strains

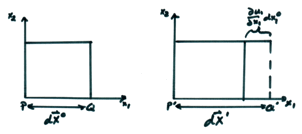
Assume only u₁ exists (i.e. u₂ = 0). Then, from equation (3)

(sum on j)

for the only non-zero component i = 1,

Since , the relative extension is

Thus, measures the relative extension along the x₁ direction. In a similar fashion, and measure the relative extensions in the x₂ and x₃ directions. The sign convention used here is,

for extension

for contraction

Also, note that strains are dimensionless.

B) Shear Strains

The off diagonal terms, , are usually called “shear strains” because they measure the local shearing. First, we will look at simple shear

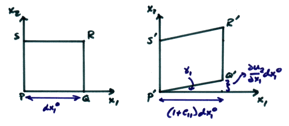
From the figure and equation (3), then

Since ,

Then,

and,

Now, from the figure

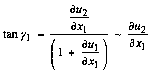
For small angles, (for small shear strains). Thus,

and, from the equation for strain

Thus, for simple strain, e₁₂ is just half the shearing angle.

The general shear strain case in 2-D is shown below.

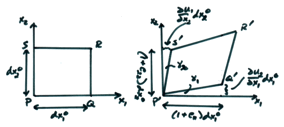
Expressing the displacements of the points Q, R, and S in terms of the displacement and its first derivatives at the point P, we can approximate

and

is the average shear angle change between line segments PQ and PS. Note that the approximations to use and require that

In fact, we require that all the strain components be infinitesimal. This is satisfied in the Earth where maximum strains associated with elastic waves are on the order of 10^-4 – 10^-5. The other shear strains e₁₃ and e₂₃ are similarly defined with respect to the different coordinate axes.

C) Rotation

In 2-D, the rotation tensor is associated with the angle of rotation of the diagonals. For example, in 2-D

where indicates rotation in the counterclockwise direction. Note that rotation does not necessarily imply shear or deformation. It is simply a local solid rotation by an angle related to Referring to the diagonal line segments from P to R and to in the figures above, simple shear has a non-zero rotation of the block. This is true for a general shear as well. Pure shear has resulting in no block rotation since then . In 3-D, we can similarly define and with respect to each pair of coordinate axes.

Dilatation

An important variable we have to define is the relative change of volume (or area in 2-D) due to the deformation. Consider again the 2-D example. If the initial area of the 2-D block is , the area of the strained block is approximately

We then define the dilatation to be

where is the divergence of the displacement field .

By a similar argument, in 3-D

The dilatation (or dilation) is the relative increase of volume due to deformation and equals the sum of the diagonal elements of the strain tensor. Thus,

where is the divergence of the displacement field.

As we shall see, the dilatation moves through the body at the P velocity.

Rotation

Another important variable useful in dealing with elastic waves is the rotation vector defined by

That is, the rotation vector is the curl of the displacement field.

In 3-D, the rotation vector describes the rotation of a material element surrounding the point P. The rotation and corresponding shear strain propagates at the velocity of shear waves (S waves) in an elastic material.

An example of the static horizontal displacement field measured geodetically after the 1927 Tango, Japan earthquake is shown in Figure 1. This shows the decay of fault parallel displacement with distance perpendicular to the fault.

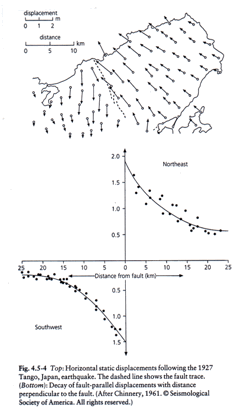
Figure 1 (from Stein and Wysession, 2003)

In the last decade, high precision GPS measurements can now attain accuracies of 10 mm in displacement and relative ground velocities of several mm/year.

Synthetic aperture radar interferometry (InSAR) uses high resolution radar mapping from spacecraft or aircraft to map the surface. By taking phase differences between images taken before and after an earthquake, very high resolution interferometric images of ground displacement can be obtained as shown in Figure 2. The top figure is a measured interferometric image of ground displacement and the bottom is from a computer model of ground displacement resulting from slip on the fault.

Figure 2 (from Stein and Wysession, 2003)