EAS 657
Geophysical Inverse Theory
Robert L. Nowack
Lecture 8
Factorizations of Ax =
y
For a set of equations Ax = y, choose a nonsingular matrix M such that
MAx = My
where MA is triangular. We want to find MA = R where
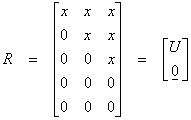
where U is square upper triangular matrix. Since M is nonsingular then A = M-1R.
Ex) A square matrix can be factored into a lower and upper triangular matrix
A = LU
This is for rapid computation of a square non-singular system Ax = y using Gaussian elimination.
Ex) For purely overdetermined systems, then we can solve this by constructing the “normal equations”
A*Ax = A*y
Where A*A is symmetric and positive definite (assuming the
eigenvalues ![]() ). Then,
). Then, ![]() can be factored as
can be factored as
![]()
where L is a lower triangular matrix and has one’s along the
main diagonal, and D is a diagonal matrix with the eigenvalues of ![]() . This is called the Cholesky
factorization of a square symmetric matrix.
This can then be used to solve by backsubstitution the normal equations
resulting from least squares.
. This is called the Cholesky
factorization of a square symmetric matrix.
This can then be used to solve by backsubstitution the normal equations
resulting from least squares.
Ex) The QR factorization
This is the preferred way to solve the purely overdetermined system. This will result in the least squares solution and works directly with the original matrix solution instead of the normal equations which may have numerical stability problems due to squared singular values.
The idea is to decompose A = Q*R, where Q is a matrix product of a series of orthogonal transformations and is unitary and
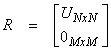
where U is a square upper triangular matrix. Now,
![]()
where QA is (MxM) (MxM) and R is (MxN). Each H is called a householder transformation. It is an orthogonal matrix of the form
![]()
Since ![]() and
and
![]()
Thus H is an orthogonal matrix. When we use a householder matrix to transform
a vector a to another vector b, then
![]()
![]()
Thus,
![]()
Ex) Find H such that 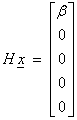 . Let
. Let
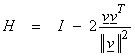
where
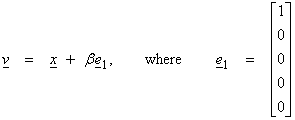
Then,
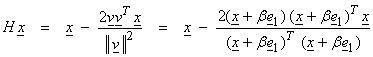
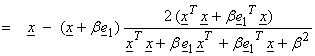
with
![]()
Then,
![]()
This is the first step of the QR alrogithm where we let
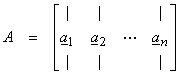
then,
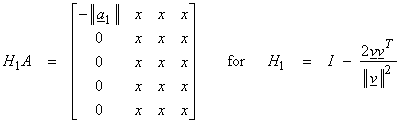
where
![]()
Now the transformations Hi are designed to zero out the elements i + 1 to M of the ith column of a partially triangularized matrix without altering the first (i-1) columns. Thus,
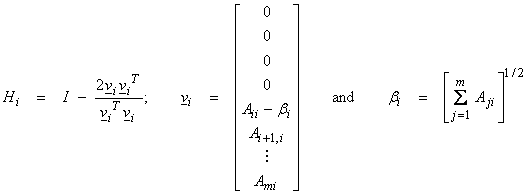
Thus,
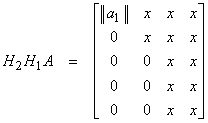
and
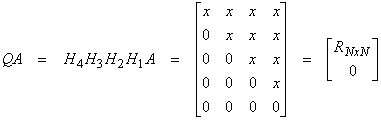
The above algorithm assumes that the A matrix is not rank deficient with P=N. If P < N, then the algorithm must be modified somewhat, with
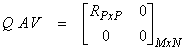
where Q is MxM, A is MxN and V is a series of householder
transformation applied on the right and is an NxN orthogonal matrix. In fact, QR type algorithms are usually first
steps in SVD algorithms. For SVD, the
final numerical step is to reduce RPxP to ![]() . But this final step
is comparatively expensive and in many cases may not be needed.
. But this final step
is comparatively expensive and in many cases may not be needed.
The most common application of the QR algorithm is to the least squares or damped least squares problem assuming a full column rank. In the least squares problem, one minimizes
![]()
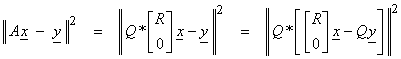
Note: length is preserved by orthogonal matrices. Then,
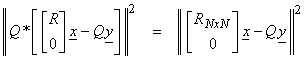
Let
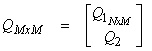
The error will be minimized by solving by back substitution for x
![]()
Ex) Damped least squares
![]()
For this case, do a Q-R decomposition on the matrix ![]() for
for
![]()
The primary
advantage of solving least squares problems with QR algorithms is not speed,
but the numerical stability in dealing with a system with eigenvalues ![]() instead of the normal
equations with eigenvalues
instead of the normal
equations with eigenvalues ![]() .
.
Operation Count for Solving Least Squares Problems with M ![]() N
N
Algorithm Flop count 1, add + 1 multiply
Normal Equations ![]()
Q-R Householder Orthogonalization ![]()
SVD ![]()