Quantum Computing and Quantum ML:
Quantum Reinforcement Learning:
Quantum Computing gives a quadratic speedup in mean estimation as compared to classical approaches. In this work, we exploit this benefit to achieve significantly better regret bounds in quantum reinforcement learning. The regret bounds become logarithmic in time as compared to square root in time with the use of quantum computing approaches.
- Bhargav Ganguly and Vaneet Aggarwal, " Quantum Acceleration of Infinite Horizon Average-Reward Reinforcement Learning ," Oct 2023.
- Bhargav Ganguly, Yulian Wu, Di Wang, and Vaneet Aggarwal, "Quantum Computing Provides Exponential Regret Improvement in Episodic Reinforcement Learning," Feb 2023.
- Yulian Wu, Chaowen Guan, Vaneet Aggarwal, and Di Wang, "Quantum Heavy-tailed Bandits," Jan 2023.
Variational Quantum Circuit for Quantum ML:
Quantum Machine Learning (QML) is an emerging research area advocating the use of
quantum computing for advancement in machine learning. Since the discovery of the capability of Parametrized Variational Quantum Circuits (VQC) to replace Artificial Neural
Networks, they have been widely adopted to different tasks in Quantum Machine Learning. However, despite their potential to outperform neural networks, VQCs are limited to
small scale applications given the challenges in scalability of quantum circuits. To address
this shortcoming, we propose an algorithm that compresses the quantum state within the
circuit using a tensor ring representation. We also show that the tensor networks have deep connections with the quantum hidden Markov models, which allow for efficient representation of tensor networks.
- Dheeraj Pedireddy, Utkarsh Priyam, and Vaneet Aggarwal, "Noisy tensor ring approximation for computing gradients of variational quantum eigensolver for combinatorial optimization," Physical Review A, Vol. 108, Iss. 4, Oct 2023
- Mohammad Ali Javidian, Vaneet Aggarwal, and Zubin Jacob, "Learning Circular Hidden Quantum Markov Models: A Tensor Network Approach," Accepted to IEEE Transactions on Quantum Engineering, Sept 2023
- Dheeraj Peddireddy, Vipul Bansal, and Vaneet Aggarwal, "Tensor Ring Parametrized Variational Quantum Circuits for
Large Scale Quantum Machine Learning," Applied Soft Computing, Volume 141, 110308, July 2023.
- Debanjan Konar, Aditya Das Sarma, Soham Bhandary, Siddhartha Bhattacharyya, Attila Cangia, Vaneet Aggarwal, "A Shallow Hybrid Classical-Quantum Spiking Feedforward Neural Network for Noise-Robust Image Classification," Applied Soft Computing, vol. 136, paper 110099, Mar 2023.
- Dheeraj Peddireddy, Vipul Bansal, Zubin Jacob, and Vaneet Aggarwal, "Tensor Ring Parametrized Variational Quantum Circuits for
Large Scale Quantum Machine Learning," in Proc. Neurips Workshop on Quantum Tensor Networks in Machine Learning, Dec. 2021.
- Mohammad Ali Javidian, Vaneet Aggarwal, and Zubin Jacob, "Tensor Rings for Learning Circular Hidden
Markov Models," in Proc. Neurips Workshop on Quantum Tensor Networks in Machine Learning, Dec. 2021.
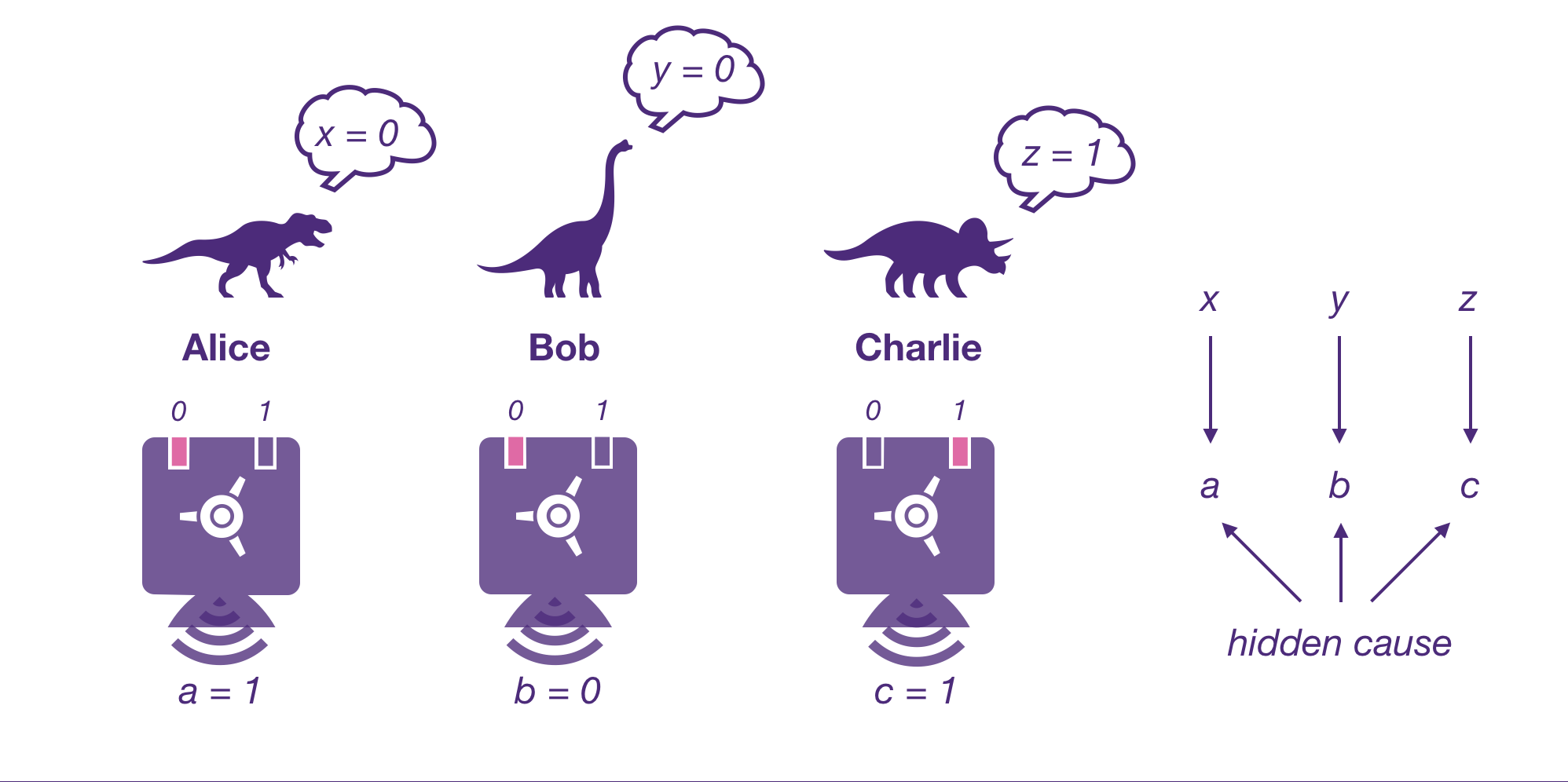
Quantum Causality:
One of the most important problems in quantum causality is linked to this prominent aphorism that states correlation does not mean causation. We proposed an approach to determine the presence of latent confounders (common causes) in quantum systems. Further, if there is no confounder, we also provide an approach to determine the cause-effect relation between the quantum systems. The approach of determining latent confounders can be applied to classical data, and is shown to outperform the algorithms for determining confounders in classical data. The key reason for the quantum approach outperforming classical approach is that the search over quantum density matrices achieve better optima than probability distributions.
- Mohammad Ali Javidian, Vaneet Aggarwal, and Zubin Jacob, "Quantum Causal Inference in the Presence of Hidden Common Causes: an Entropic Approach," Physical Review A, 106, 062425, Dec 2022.
- Mohammad Ali Javidian, Vaneet Aggarwal, Fanglin Bao, and Zubin Jacob, "Quantum Entropic Causal Inference," Feb 2021
- Mohammad Ali Javidian, Vaneet Aggarwal, and Zubin Jacob, "Identification of Latent Graphs: A Quantum Entropic Approach," in Proc. Neurips Workshop on Causal Inference & Machine Learning WHY-21, Dec. 2021.
- Mohammad Ali Javidian, Vaneet Aggarwal, and Zubin Jacob, "Quantum Causal Inference: an Entropic Approach," in Proc. UAI Workshop, Jul 2021.
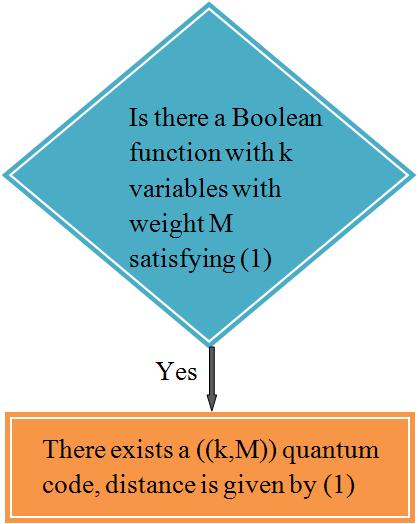
Boolean functions and Projection Operators:
There is a fundamental correspondence between Boolean functions and projection operators in Hilbert space. I have used it to provide a common mathematical framework for the design of both additive and non-additive quantum error correcting codes and to construct new families of error correcting codes. As shown in the figure alongside, the problem of finding new quantum codes is converted to a problem of finding a boolean function satisfying certain properties; thus converting the problem of finding quantum codes to a classical problem. The correspondence is widely applicable and I have also used it to construct and analyze new families of non-coherent space-time codes for applications in wireless communication.
- V. Aggarwal
and A. R. Calderbank, "Boolean
Functions, Projection Operators, and Quantum Error Correcting Codes," IEEE Trans. on
Inf. Th., vol. 54, no. 4, Apr. 2008, pp. 1700-1707.
- V. Aggarwal
and A. R. Calderbank, "Boolean Functions, Projection Operators
and Quantum Error Correcting Codes," in Proc. International Symposium on Information
Theory, pp.2091-2095, June 2007, Nice.
- V. Aggarwal, A. Ashikhmin and A. R. Calderbank, "A
Grassmannian Packing Based on the Nordstrom-Robinson Code", in Proc. Information Theory Workshop, pp. 1-5, Oct. 2006, Chengdu,
China.
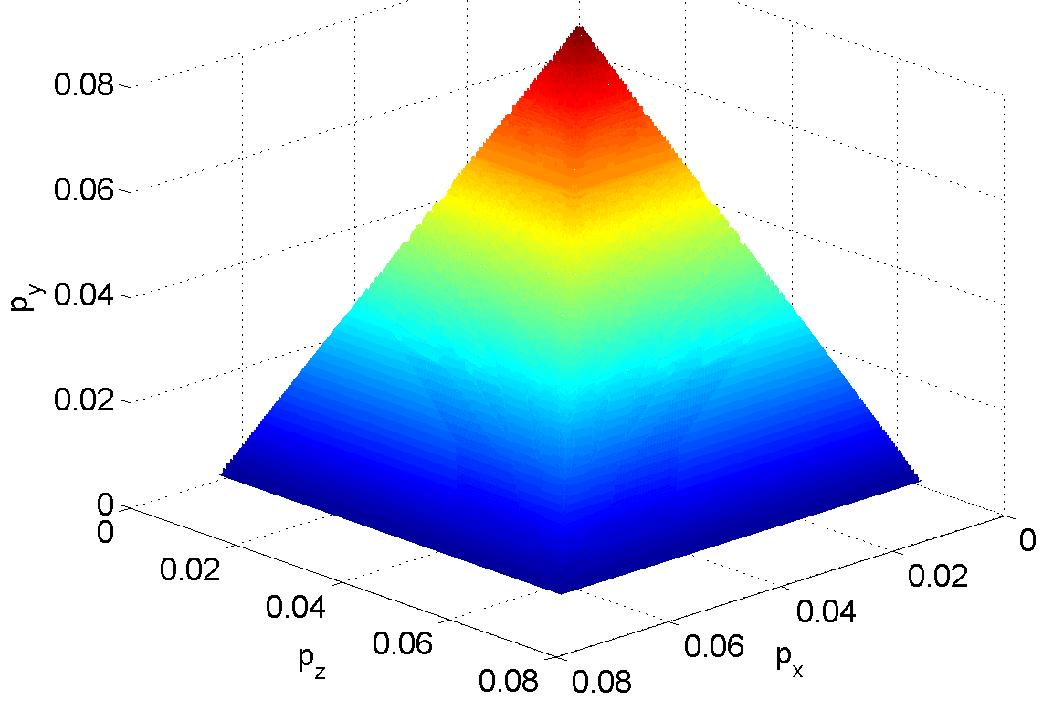
Quantum Fault Tolerance:
I am interested in understanding how to reliably determine error thresholds that are both necessary and sufficient to support fault tolerant quantum computing. The standard approach to quantum fault tolerance is to calculate error thresholds on basic gates in the limit of arbitrarily many concatenation levels. I want to be able to take the number of qubits and the target implementation accuracy as a constraint and then provide a framework for engineering the constrained quantum system to the required tolerance. I have developed a different approach which is based on complete analytical solutions to the dynamics of quantum error correction. I believe it will result in better integration of hardware and software since the full error manifold clarifies what is easier to do in physics and what is easier to do in error control algorithms. As an example, the image on the right shows the manifold of initial error probabilities that are consistent with a given implementation inaccuracy when the 7-qubit code is concatenated a specified number of times. My research program was funded by DARPA under the highly competitive QuEST Program.
- V. Aggarwal, A. R. Calderbank, G. Gilbert and Y. S. Weinstein, "Volume Thresholds for Quantum Fault Tolerance",
Quantum Information Processing, Volume 9 Issue 5, October 2010.
- V. Aggarwal, A. R. Calderbank, G. Gilbert and Y. S. Weinstein, "Analyses of Volume Thresholds in Quantum Fault Tolerance," in Proc. APS March Meeting 2010.
- V. Aggarwal, A. R. Calderbank, G. Gilbert and Y. S. Weinstein, "Engineering Fault Tolerance for Realistic Quantum Systems via the Full Error Dynamics of Quantum Codes," in Proc. ISIT, Seoul, Korea, Jun.-Jul. 2009.
- G. Gilbert, Y. S. Weinstein, V. Aggarwal and A. Robert Calderbank, "Operator Theoretic Quantum Fault Tolerance," in Proc. APS March Meeting 2009.
- V. Aggarwal,
A. R. Calderbank, G. Gilbert, M. Hamrick and Y.
S. Weinstein, "A Universal
Operator Theoretic Framework for Quantum Fault Tolerance," in
Proc. APS March Meeting 2008.
- G. Gilbert, M. Hamrick,
Y. S. Weinstein, V. Aggarwal and A. R. Calderbank, "A
Universal Operator Theoretic Framework for Quantum Fault Tolerance",
arXiv:0709.0128, Sept. 2007.
Home



