Tensor Networks:

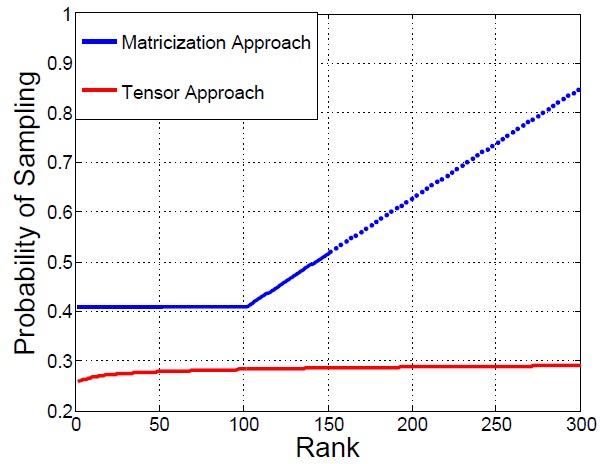
Tensors are generalizations of vectors and matrices; a vector is a first-order tensor and a matrix is a second-order tensor. Most of the data around us are better represented with multiple orders to capture the correlations across different attributes. For example, a color image can be considered as a third-order tensor, two of the dimensions (rows and columns) being spatial, and the third being spectral (color), while a color video sequence can be considered as an order four tensor, time being the fourth dimension besides spatial and spectral. Similarly, a colored 3-D MRI image across time can be considered as an order five tensor. Exploiting additional structure leads to better embedding algorithms for subspace analysis and the elements needed for data completion (as shown alongside).

• M. Ashraphijuo, X. Wang, and V. Aggarwal, "Fundamental sampling patterns for low-rank multi-view data completion," Pattern Recognition, vol. 103, Jul 2020.
• X. Liu, S. Aeron, V. Aggarwal, and X. Wang, "Low-tubal-rank Tensor Completion using Alternating Minimization," IEEE Transactions on Information Theory, vol. 66, no. 3, pp. 1714-1737, March 2020.
• W. Wang, Y. Sun, B. Eriksson, W. Wang, and V. Aggarwal, "Wide Compression: Tensor Ring Nets," in Proc. CVPR, Jun 2018 (29% acceptance rate).
• W.Wang, V. Aggarwal, and S. Aeron, "Efficient Low Rank Tensor Ring Completion," in Proc. ICCV, Oct 2017 (28.9% acceptance rate).
• W.Wang, V. Aggarwal, and S. Aeron, "Unsupervised Clustering Under The Union of Polyhedral Cones (UOPC) Model," Pattern Recognition Letters, vol. 100, pp. 104-109, Dec 2017.
• M. Ashraphijuo, V. Aggarwal, and X. Wang, "Deterministic and Probabilistic Conditions for Finite Completability of Low-Tucker-Rank Tensor," IEEE Transactions on Information Theory, vol. 65, no. 9, pp. 5380-5400, Sept. 2019.
• W. Wang, V. Aggarwal, and S. Aeron, "Tensor Train Neighborhood Preserving Embedding," IEEE Transactions on Signal Processing, vol. 66, no. 10, pp. 2724-2732, May, 2018.
• M. Ashraphijuo, V. Aggarwal, and X. Wang, "On Deterministic Sampling Patterns for Robust Low-Rank Matrix Completion," IEEE Signal Processing Letters, vol. 25. no. 3, pp. 343-347, Mar 2018.
• M. Ashraphijuo, X. Wang, and V. Aggarwal, "Rank Determination for Low-Rank Data Completion," Journal of Machine Learning Research, vol. 18(98), pp. 1-29, Sept 2017.
• M. Ashraphijuo, X. Wang, and V. Aggarwal,"An approximation of the CP-rank of a partially sampled tensor," in Proc. Allerton, Oct 2017.
• M. Ashraphijuo, V. Aggarwal, and X. Wang, "A characterization of sampling patterns for low-tucker-rank tensor completion problem," in Proc. IEEE ISIT, Jun 2017.
• M. Ashraphijuo, X. Wang, and V. Aggarwal,"A characterization of sampling patterns for low-rank multi-view data completion problem," in Proc. IEEE ISIT, Jun 2017.
• V. Aggarwal, A. A. Mahimkar, H. Ma, Z. Zhang, S. Aeron, and W. Willinger, "Inferring Smartphone Service Quality using Tensor Methods," in Proc. 12th International Conference on Network and Service Management Oct-Nov, 2016.
• X. Liu, S. Aeron, V. Aggarwal, X. Wang, and M. Wu, "Adaptive Sampling of RF fingerprints for Fine-grained Indoor Localization," IEEE Transactions on Mobile Computing, vol. 15, no. 10, pp. 2411-2423, Oct. 2016.
• V. Aggarwal and S. Aeron, "A note on Information-theoretic Bounds on Matrix Completion under Union of Subspaces Model," in Proc. Allerton, Sept 2016.
• W.Wang, S. Aeron, and V. Aggarwal, "On deterministic conditions for subspace clustering under missing data," in Proc. IEEE ISIT, 2016.
• X. Liu, S. Aeron, V. Aggarwal, and X. Wang, "Low-tubal-rank Tensor Completion using Alternating Minimization," in Proc. SPIE Defense + Security, 2016.
• X. Liu, S. Aeron, V. Aggarwal, X. Wang, and M. Wu, "Tensor completion via adaptive sampling of tensor fibers: An application to efficient RF fingerprinting," in Proc. IEEE ICASSP, Mar 2016.