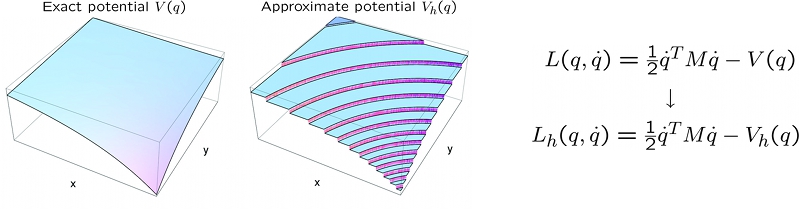
We present a class of integration schemes for Lagrangian mechanics, referred to as energy-stepping integrators, that are momentum and energy conserving, symplectic and convergent. In order to achieve these properties we replace the original potential energy by a piecewise constant, or terraced approximation at steps of uniform height. By taking steps of diminishing height, an approximating sequence of energies is generated. The trajectories of the resulting approximating Lagrangians can be characterized explicitly and consist of intervals of piecewise rectilinear motion. 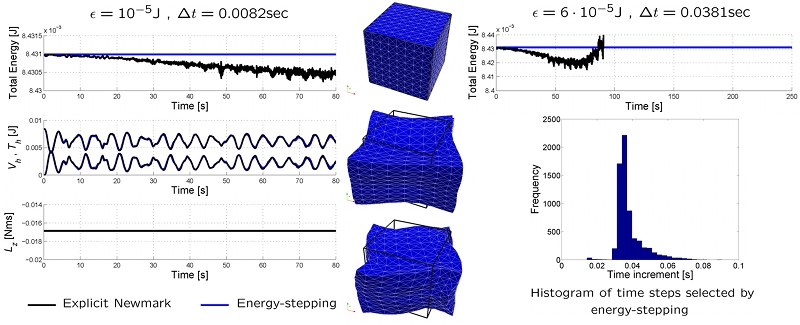We show that the energy-stepping trajectories are symplectic, exactly conserve all the momentum maps of the original system and, subject to a transversality condition, converge to trajectories of the original system when the energy step is decreased to zero. These properties, the excellent long-term behavior of energy-stepping and its automatic time-step selection property are born out by selected examples of application, including the dynamics of a frozen Argon cluster, the spinning of an elastic cube and the collision of two elastic spheres.