|
Three-D Earth Structure Model 1 Larry Braile Professor,
http://web.ics.purdue.edu/~braile/)
Sheryl Braile Teacher, Happy May, 2000 (revised
February, 2002, September, 2005) |
|
Objective: Construct a 3-D model of the interior of the Earth to help visualize the main spherical* layers or regions -- inner core, outer core, mantle and crust. This project reinforces the concepts included in the Earth’s Interior Structure activity** by utilizing a 3-dimensional model to enhance visualization and illustration of the relative volumes of Earth’s layers. This activity also provides an opportunity for some practice in problem solving and math skills.
Two options for the
materials used to make the 3-D models are described. The baker’s clay option has the following
advantages: 1) It is less expensive and
the materials are easier to obtain. 2)
The baker’s clay is easy to work with and results in a model Earth that, when
baked is relatively permanent and “rugged.”
3) The “estimating” and “dividing” activities are easier to perform with
the baker’s clay. The disadvantages of
the baker’s clay are: 1) The making of
the baker’s clay and the mixing of food coloring are “messy” activities,
especially for students. 2) It is difficult
to make an Earth model with the baker’s clay in which the layers are reasonably
spherical and the boundaries between layers are reasonably sharp. Using the modeling clay has the following
advantages: 1) The resulting models are
more accurate, including nearly spherical layers and sharp boundaries between
layers. Very little preparation of the
materials is necessary and working with the modeling clay does not make a
mess. The disadvantages of the modeling
clay are higher cost and greater difficulty in performing the “estimating” and
“dividing” problem solving activities.
Materials:
Option 1: Baker’s Clay
Baker’s
clay mix*** Aluminum
foil
Red and yellow food
coloring Kitchen
knife
Saran wrap Poster
paint
Electronic
scale, triplebeam Meter
stick
balance or spring scale
capable of measuring up to
500g of mass to an accuracy
of 1g (0.1g preferred)
Option
2: Modeling Clay
4 colors of modeling clay Poster paint
Aluminum foil Meter stick
Electronic scale, triplebeam Kitchen knife
balance or spring scale
capable of measuring up to
500g of mass to an accuracy
of 1g (0.1g preferred)
(You will need different volumes of different colors of the modeling clay to correspond to the relative volumes of the Earth’s spherical layers. We have used about 300g of gray modeling clay obtained from the university “stores” supply (or a craft store) for about $2/kg for the estimating activity and for the mantle “layer” of the final 3-D model. Additional colored clay (a 450g box containing four colors - green, yellow, red, blue - and costing $2) was obtained from Wal-Mart. If you have the students work in pairs and each student gets to keep one half of the 3-D Earth model, you will need about 300g of gray clay and one half box of the (4-color) clay for each pair of students. There will be some extra clay. A 300g Earth model can be made from 246g of gray clay for the mantle, 47.1g of yellow clay for the outer core, 4.8g of blue clay for the crust, and 2.1g of red clay for the inner core. Dividing the clay into these volumes may be performed as a problem solving exercise in which measuring the mass is only one method that can be used. If this “dividing the clay” into the correct volumes activity is performed as a problem solving exercise, you may wish to use the 300g of gray clay to initially form the volumes and then replace the smaller volumes with the equivalent volumes of colored clay. You will find that the modeling clay is easier to work with if it is softened by heating in a microwave oven. Experiment with a small amount of time in the microwave first.)
Procedure (Option 1): Mix one batch of Baker’s clay (see recipe) for each student or pair of students. (If students work in pairs, they may each keep 1/2 of the 3-D Earth model.) As an “estimating” activity, divide the clay into four volumes corresponding to what you expect to be the relative volumes of the four main regions or layers of the Earth’s interior – inner core, outer core, mantle, crust.
Examine the relative volumes (calculated for the Earth) of these layers
shown in Table 1. Do your estimates of
volume agree with the actual volumes?
How do you find out? (The scale
or volume estimation methods may be used to answer this question.)
Split the clay into volumes according to the relative percentages given
on the attached page. (There are several
efficient and relatively accurate methods to divide the clay into these
volumes. For example, split into 10
approximately equal spheres (10% volume each), then split one or more of the 10
spheres into 10 approximately equal spheres (1% volume each). Or, roll into a long cylindrical shape, use
the meter stick to measure out percentages of the total length and cut the
cylinder. You may wish to
"problem-solve" this part of the activity as an additional
objective.) Roll the smallest volume
(representing the inner core) into a sphere and color this amount red by mixing
in food coloring. Cover with saran wrap
until ready to use. Color the outer core
clay yellow and the mantle clay orange; leave the clay for the crust
white. Cover clay until ready to use.
To construct the 3-D model, first roll each of the volumes into a
sphere. Then, cut the outer core
sphere exactly in half. In each half,
press a hemispherical hole into the middle of the flat side of each half with
your finger or thumb. This hole should
be large enough to accept one half of the inner core sphere. Now place the inner core sphere inside the
two halves of the outer core sphere to make one larger sphere. Now, cut the mantle sphere exactly in half
and repeat the process just completed, to form concentric spheres - inner core
inside the outer core which is inside the mantle. Press evenly on the outside of the mantle
sphere to firmly attach all of the spherical layers.
Try to flatten the clay for the crust sufficiently to cover the surface
of the mantle. (You won’t be able to do
this, so set the crust clay aside. At
this scale, the crustal layer will be only a small fraction of a millimeter
thick, so we will “paint on” the crust after the clay is baked. However, attempting to flatten the clay for
the crust will emphasize the relatively small thickness and volume of the
crustal layer and the concept of scale.)
Cut the 3-D clay Earth model
in half. You should be able to see the
interior layering, and the relative volumes of the main layers will be more
understandable after constructing the model.
(If inner core is not visible after cutting, dig out the inner core and
reshape to approximate concentric hemispherical layers.) Bake the halves of the model Earth on foil
(flat side down) in a 200 degree F (~94 degrees C) oven until dried. (This may take 24 hours or more). Paint the spherical exterior to represent the
crustal layer. An additional coating of
acrylic or polymer will protect the painted surface (optional).
Procedure (Option 2): Provide each student team with 300g of gray clay. You may wish to soften the clay to make it easier to divide and to form into spheres. Ask the team to divide the clay into 4 volumes that represent the relative volumes of the four main regions or layers of Earth’s interior - inner core, outer core, mantle, and crust.
Examine the relative volumes (calculated for the Earth) of these layers shown in Table 1. Do your estimates of volume agree with the actual volumes? How do you find out?
Next, divide the 300g of clay into volumes corresponding to the percentages of Earth’s layers - inner core, outer core, mantle, crust - as shown in Table 1. You may wish to “problem-solve” this procedure. There are several methods for performing this division and the students could be challenged to think of at least two or three of these methods. Of course, using mass measured on a scale is one of the easiest. If the whole Earth is represented by 300g of clay, then the masses of the various volumes are: inner core, 2.1g; outer core, 47.1g; mantle, 246g; and crust, 4.8g (Figure 1).
Now replace the gray clay for the inner and outer core with equal volumes (masses) of red and yellow clay, respectively. Also replace the gray clay for the crust with an equal volume (mass) of blue clay (Figure 2).
To complete the 3-D Earth model, use the same construction procedure as described above for the baker’s clay. The completed model should be cut in half and each student can keep one half. The spherical shells and boundaries between the layers should be easily visible in the 3-D model.
Results: Note that in the cross section view of the Earth (Figures 3 and 4), the mantle does not appear to be a significantly larger region than the core. However, because of the 3-D, spherical shape of the Earth and its inner layers (and the resulting R3 volume relationship described below), the mantle is actually 82% of the Earth by volume. Because the mantle and crust are silicate rocks (silicon- and oxygen-rich minerals) in contrast to the much smaller core which is made up of iron, the Earth is primarily a silicate rock planet.
Extensions/Enrichment:
1. Compare the 3-D Earth model to the Earth’s Interior Structure
“slice” of the Earth and the Earth’s Anatomy poster (http://www.tufts.edu/as/wright_center/svl/posters/erth.html; see Figure 11). What is the approximate scale of the 3-D
clay Earth model?
2. Additional information on the Earth's interior can be found
in: Bolt, B.A., Earthquakes and
Geological Discovery, W.H. Freeman and Co.,
3. Determine how to calculate the volume of
each of the spherical layers or shells using the formula for the volume of a
sphere, V = ![]() pR3. Given the radius of the bottom (Rb) and radius of the top (Rt) of a spherical shell
(Figure 5), the volume of the layer is:
pR3. Given the radius of the bottom (Rb) and radius of the top (Rt) of a spherical shell
(Figure 5), the volume of the layer is:
![]()
or,
![]()
For example, for the Earth's mantle,
Rb = 3486 km, Rt
= 6336 km, so,
V = ![]() (63363 - 34863) km3
(63363 - 34863) km3
V » 8.880 x 1011 km3 (or
approximately 888,000,000,000 km3 or 888 billion cubic km).
The total volume of the Earth
is (approximately) 10.83 x 1011 km3, so the relative volume of
the mantle (as compared to the volume of the whole Earth) is ~82%.
4. Find estimates of the
average density of the 4 main regions of the Earth - inner core, outer core,
mantle, crust. The book by Bolt,
referenced above, is a good source, or, you may want to perform an Internet
search for this information. (An
activity exploring the density of materials, rocks and minerals would also be a
good preparatory or follow-up lesson to the 3-D Earth model construction.) Using the density estimates, calculate the
relative masses of the 4 regions of the Earth.
Do these relative masses differ significantly from the relative volumes
that we have used to construct the 3-D Earth model? Why have we chosen to construct the model
using relative volumes rather than relative masses?
5. Additional Earth’s interior structure
activities are: Earth’s Interior Structure (http://web.ics.purdue.edu/~braile/edumod/earthint/earthint.htm),
Journey to the Center of the Earth (http://web.ics.purdue.edu/~braile/edumod/journey/journey.htm),
and Earth’s Interior
Structure – Seismic Travel Times in a Constant Velocity Earth (http://web.ics.purdue.edu/~braile/edumod/constvel/constvel.htm).
6. A foam, scale model of Earth
structure (Figures 6 and 7) can be purchased at: http://www.etacuisenaire.com/. What is the approximate scale of the foam
model Earth?
7. An ice cream model of
Earth’s interior can be constructed using ice cream and a large mixing bowl
which has an approximate hemisphere shape.
Use, a one-half gallon container of chocolate ice cream and a one-half
gallon container of Neapolitan (vanilla, chocolate and strawberry) ice cream. Scoop all of the chocolate ice cream into the
bowl to make the Earth’s mantle including a hemisphere hole for the Earth’s
outer core. Line the hole with
strawberry ice cream to represent the outer core leaving a small hemisphere
hole for the inner core (Figure 8).
Return the ice cream to the freezer to let it become solid. Dip the bowl in warm water for a few seconds
to loosen the ice cream and place the ice cream Earth model on a flat surface
with the flat side down. Whipped cream
or Cool Whip (colored with food coloring) can be used to add the Earth’s crust
and approximate continental regions can be indicated by the colored whipped
cream (Figure 9). By cutting a quarter
of the hemisphere out of the ice cream model, one can see the Earth’s interior
layers (Figure 10). Of course, one can
then serve pieces of the ice cream Earth model for a smack or treat.
*The Earth is
actually not quite spherical. Because
the Earth is rotating about its axis, and because Earth materials (rocks) are
not perfectly rigid, the Earth is approximately an ellipsoid. The polar radius (6357 km) is about 21 km
smaller than the equatorial radius (6378 km).
However, this "flattening" of the Earth into an ellipsoid is
relatively small (~ 0.3%). Thus, it is
common to consider the Earth to be approximately spherical with a radius of
6371 km (the radius of a sphere of equal volume to the ellipsoidal Earth). Furthermore, the thickness of the Earth's
crust (and therefore the radius at the top of the mantle) is quite variable;
averaging about 35 km in continental regions and about 5 km, plus 4 km of
water, in ocean regions. In mountainous
areas, the continental crust is up to 70 km thick. However, at the scale of the 3-D model, these
variations are negligible and a smooth, nearly spherical surface for the top of
the mantle is a good approximation.
**“Earth’s Interior
Structure”,L. Braile (http://web.ics.purdue.edu/~braile/edumod/earthint/earthint.htm).
A similar
Earth's interior activity is: "Crust
to Core: A Pizza the Earth”, Tremor Troop: Earthquakes - A Teacher's Package
for K-6, NSTA/FEMA, p. 54-55, 1987.
(Note misprint of scale on page 55; the correct scale is 1 millimeter to
10 kilometers, or
Baker’s Clay
Recipe***
2 cups flour
1/2 cup salt
3/4 cup water (this amount varies with humidity)
Mix flour and salt.
Add 1/2 cup water. Mix with
hands. Add additional water until
mixture forms ball. Knead until salt
feels dissolved (about five minutes).
Results are best if clay mixture is very firm (not overly
moist) and smooth.
Cover or put in plastic bag until ready to use. When objects are ready, place on foil-covered
cookie sheet. Bake in preheated oven at
200 degrees F (~ 94 degrees C). Allow to
bake approximately one-hour for every 1 cm of dough thickness.
***Keep dough mixture under
cover or plastic bag because it dries out rapidly in air.
Table 1: Crust, Mantle and Core of the Earth
|
Layer |
Radius (km) |
Relative Volume (%) |
Suggested Color |
Composition of Layer in the Earth |
|
Inner Core |
0 - 1216 |
0.7 |
Red |
Solid Iron |
|
Outer Core |
1216 - 3486 |
15.7 |
Yellow |
Liquid Iron |
|
Mantle |
3486 - 6336 |
82.0 |
|
Iron and Magnesium rich silicate rock |
|
Crust |
6336 - 6371 |
1.6 |
White or blue |
Silica (SiO2) rich rocks |

Figure 1.
Photograph of spheres of clay representing the relative volumes of the
layers of the Earth's interior.

Figure 2. Photograph of colored spheres of clay with
volumes and colors representing the Earth's inner core, outer core, mantle and
crust as shown in Table 1.

Figure 3.
Photograph of a completed 3-D Earth model made from modeling clay. The model has been cut in half so that the
inner layers (spherical shells) are visible.
A piece of clay representing the volume of the Earth's crust has been
flattened and is shown to the right of the 3-D model. We discover that the volume of crust is so
small, that we cannot roll out the clay thin enough to make the outer shell of
the 3-D model Earth.
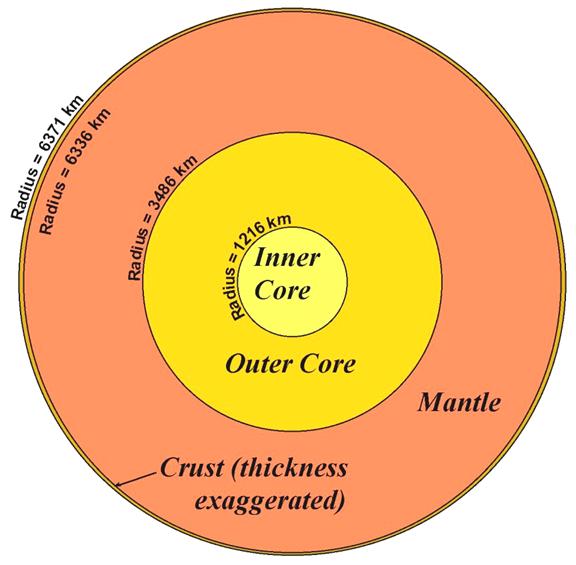
Figure 4.
Schematic diagram illustrating the major spherical shells of the Earth's
interior structure. The circles
(representing spherical shells in the 3-D model) are drawn at true scale except
for the circle representing the base of the crust. The thickness of the crustal layer is
exaggerated so that a distinct layer is visible at this scale (the scale of
this diagram is approximately 1:90 million).
In the real Earth, the crust is also of variable thickness with
significant differences between the crustal thickness of oceanic and
continental regions and increased crustal thickness beneath mountainous areas.
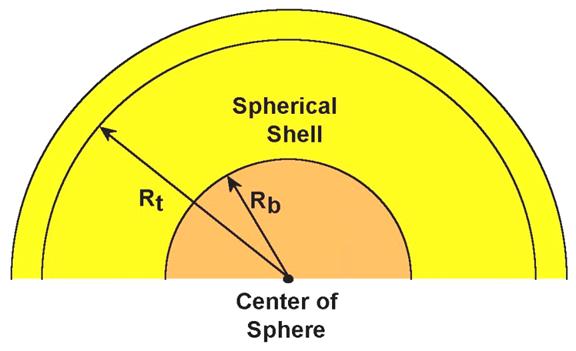
Figure 5.
Schematic diagram illustrating spherical shells or layers and the radii
(Rt and Rb) that allow one to calculate the volume of the
spherical shell by calculating the volume of a sphere of radius Rt
and subtracting the volume of a sphere of radius Rb. These calculations are detailed in the
Extension/Enrichment section.

Figure 6.
Photograph of commercial, foam, scale model of the Earth..

Figure 7.
Photograph of commercial, foam, scale model of the Earth showing the
Earth’s interior structure (the three rectangular tabs and holes are to align
the two halves correctly when pieced together as a sphere; the thickness of the
crust is exaggerated in the model).

Figure 8.
Ice cream model of the Earth’s interior representing one hemisphere.

Figure 9.
Ice cream Earth model with continent and ocean regions added to surface.

Figure 10.
Ice cream Earth model showing interior structure.
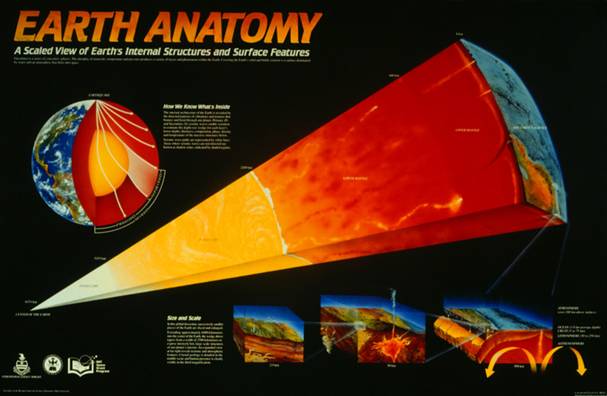
Figure 11. Earth Anatomy poster from
[1]  Last
modified March 15, 2006
Last
modified March 15, 2006
The web page for
this document is:
http://web.ics.purdue.edu/~braile/edumod/threedearth/threedearth.htm
Partial funding for this development provided by the National Science Foundation.
ã Copyright 2002-2006. L. Braile. Permission granted for reproduction for non-commercial uses.