Wireless Communication Networks:
PhD Dissertation
The use of wireless technology is rapidly growing. The demand is so huge that the limited supply of resources is becoming the bottleneck. Thus, network designs need to be rethought. Most of the analyses to date consider complete network information, perfect knowledge of channel state at the receivers, perfect knowledge of location of destination or perfect feedback link. This is an idealization and new design strategies accounting for the imperfect or incomplete information are needed. In this thesis, we will consider the effect of various forms of incomplete and imperfect knowledge motivated by practical protocol designs. The basic theme of the results is an old adage ``If we know more, we can achieve more." This thesis applies this adage to networks, where more information about the network translates into higher throughput or diversity.
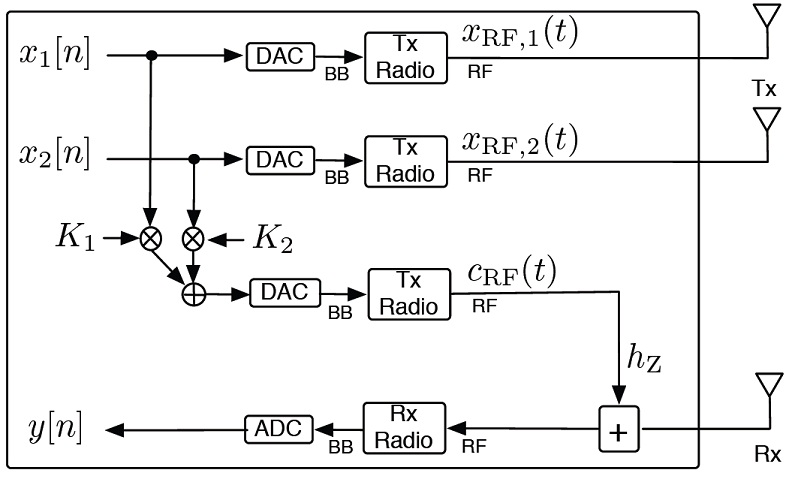
Full-Duplex Wireless Communications:
The graphic alongside depicts a design of a full-duplex radio design that can be used for self-interference cancellation. I worked on some innovations at the physical and MAC layers for full-duplex communication systems for applications in indoor as well as outdoor environments
- M. Ashraphijuo, V. Aggarwal, and X. Wang, "The DoF of Two-way Butterfly Networks," IEEE Communications Letters, vol. 21, no. 10, pp. 2254-2257, Oct 2017.
- M. Ashraphijuo, V. Aggarwal, and X. Wang, "On the DoF of Two-way 2x2x2 Relay Networks with or without Relay Caching," IET Communications, Volume 11, Issue 13, pp. 2089 – 2094, Sept 2017.
- M. Ashraphijuo, V. Aggarwal, and X. Wang, "On the Capacity Regions of Two-Way Diamond Channels," IEEE Trans. Inf. Th., vol.61, no.11, pp.6060-6090, Nov. 2015.
- M. Ashraphijuo, V. Aggarwal, and X. Wang, "Capacity of Two-Way Linear Deterministic Diamond Channel," in Proc. IEEE ISIT, Jun. 2015.
- V. Aggarwal, and N. K. Shankaranarayanan, “Performance of a Random-Access Wireless Network
with with a mix of full- and half-duplex stations,” IEEE Trans. Communications Letters, vol. 17, no. 11,
Nov. 2013.
- M. Duarte, A. Sabharwal, V. Aggarwal, R. Jana, K. K. Ramakrishnan, C. Rice, and N. K. Shankaranarayanan, “Design and Characterization of a Full-duplex Multi-antenna System for WiFi networks,” IEEE Trans. Vehicular Technologies, vol.63, no.3, pp.1160-1177, March 2014. (2017 Jack Neubauer Memorial Award recognizing the Best Systems Paper published in the IEEE Transactions on Vehicular Technology)
- V. Aggarwal, M. Duarte, A. Sabharwal, and N. K. Shankaranarayanan, “Full- or Half-Duplex? A Capacity Analysis with Bounded Radio Resources,” in Proc. IEEE Information Theory Workshop, Sept. 2012.
- Other patent submissions on the topic with applications to WiFi and cellular technologies can be seen in my CV.
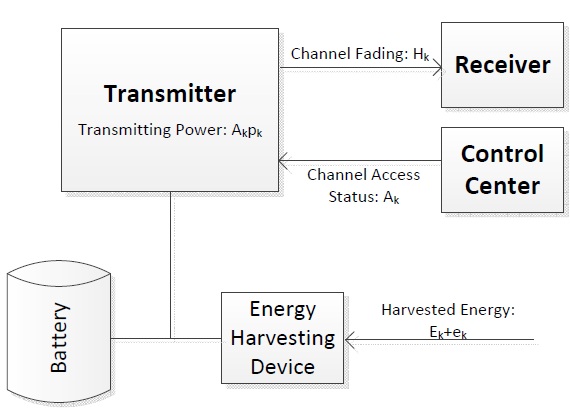
Communication with Energy Harvesting Devices:
The utilization of renewable energy is an important characteristic of the green wireless communication, making the flexible deployment of the transmitters and reducing the consumption of the fossil energy. If the devices are powered with renewable energy sources, what are the best approaches for communication accounting for the limited battery capacity. The figure alongside gives a pictorial representation of a energy harvesting device with battery. I investigated new scheduling approaches with renewable energy. In the presence of non-causal information for energy harvesting and the channel state information, we give a dynamic water-filling algorithm that is optimal. Since the non-causal channel state information may be less practical, I consider a reverse water-filling algorithm with causal information of the channel states. I also gave an approximately optimal solution that works with complete causal information. Further, the results have been extended to multiple users. Surprisingly, for the case of multiple interfering links, we find that frequency splitting is essential with finite battery capacity which is not the case with just average power constraint.
- M. Rezaee, M. Mirmohseni, V. Aggarwal, and M. R. Aref, "Optimal Transmission Policies for Multi-hop Energy Harvesting Systems," IEEE Transactions on Green Communications and Networking, vol. 2, no. 3, pp. 751-763, Sept. 2018.
- V. Aggarwal, X. Wang, and Z. Wang, "Joint Energy-Bandwidth Allocation for Multiple Broadcast Channels with Energy Harvesting," Chapter in "Cognitive Radio Networks: Performance, Applications and Technology" published by Nova Science Publishers, 1st quarter, 2018.
- V. Aggarwal, Z. Wang, X. Wang, and M. Ismail, "Energy Scheduling for Optical Channels with Energy Harvesting Devices," IEEE Transactions on Green Communications and Networking, vol. 2, no. 1, pp. 154-162, Mar 2018.
- V. Aggarwal, M. R. Bell, A. Elgabli, X. Wang, and S. Zhong, "Joint Energy- Bandwidth Allocation for Multi-User Channels with Cooperating Hybrid Energy Nodes," IEEE Transactions on Vehicular Technology, vol. 66, no. 11, pp. 9880-9889, Nov. 2017.
- V. Aggarwal, M. R. Bell, A. Elgabli, X. Wang, and S. Zhong, "Joint Energy- Bandwidth Allocation for Multi-User Channels with Cooperating Hybrid Energy Nodes," in Proc. IEEE ICC (Green Communications Systems and Networks Symposium), May 2017.
- Z. Wang, V. Aggarwal, X. Wang, and M. Ismail, "Energy Scheduling for Optical Channels with Energy Harvesting Devices," in Proc. IEEE ICC (Green Communications Systems and Networks Symposium), May 2017.
- Z. Wang, V. Aggarwal, and Xiaodong Wang, "Optimal Energy-Bandwidth Allocation for Energy-Harvesting Networks in Multiuser Fading Channels," IEEE Journal on Selected Areas in Communications, vol. 34, no. 5, pp. 1565-1577, May 2016.
- Z. Wang, V. Aggarwal, and X. Wang, "Transmission with Energy Harvesting Nodes in Frequency-Selective Fading Channels," IEEE Transactions on Wireless Communications, vol. 15, no. 3, pp. 1642-1656, March 2016.
- M. Ashraphijuo, V. Aggarwal, and X. Wang, "On the Capacity of Energy Harvesting
Communication Link," IEEE JSAC, vol. 33, no. 12, pp. 2671-2686, Dec. 2015.
- Z. Wang, V. Aggarwal, and X. Wang, "Joint Energy-Bandwidth Allocation in Multiple
Broadcast Channels with Energy Harvesting," IEEE Transactions on Communications, vol.63, no.10, pp.3842-3855, Oct. 2015.
- M. Ashraphijuo, V. Aggarwal, and X. Wang, "Energy Harvesting Communication Using Limited
Battery with Efficiency," in Proc. Allerton Conference on Communication, Control, and Computing, Oct 2015.
- Z. Wang, V. Aggarwal, and X. Wang, "Energy-Subchannel Allocation for Energy Harvesting Nodes in Frequency-Selective Channels, in Proc. IEEE ISIT, Jun. 2015
- Z. Wang, V. Aggarwal, and X. Wang, "Energy-Bandwidth Allocation in Multiple Orthogonal Broadcast Channels with Energy Harvesting, in Proc. IEEE ISIT, Jun. 2015
- Z. Wang, V. Aggarwal, and X. Wang, "Iterative Dynamic Water-filling for Fading Multiple-Access Channels with Energy Harvesting," IEEE J-SAC Special Issue on Wireless Communications Powered by Energy Harvesting and Wireless Energy Transfer, vol.33, no.3, pp.382-395, Mar
2015.
- Z. Wang, V. Aggarwal, and X. Wang, "Energy Allocation for Energy Harvesting Transmitter
with Causal Information," IEEE Trans. Communications, vol.62, no.11, pp.4080-4093, Nov. 2014.
- Z. Wang, V. Aggarwal, and X. Wang, "Optimal Energy-Bandwidth Allocation for Energy Harvesting Interference Networks, in Proc. IEEE ISIT, Jul. 2014
- Z. Wang, V. Aggarwal, and X. Wang, " Renewable Energy Scheduling for Fading Channels with Maximum Power Constraint," in Proc. Allerton, Oct. 2013.
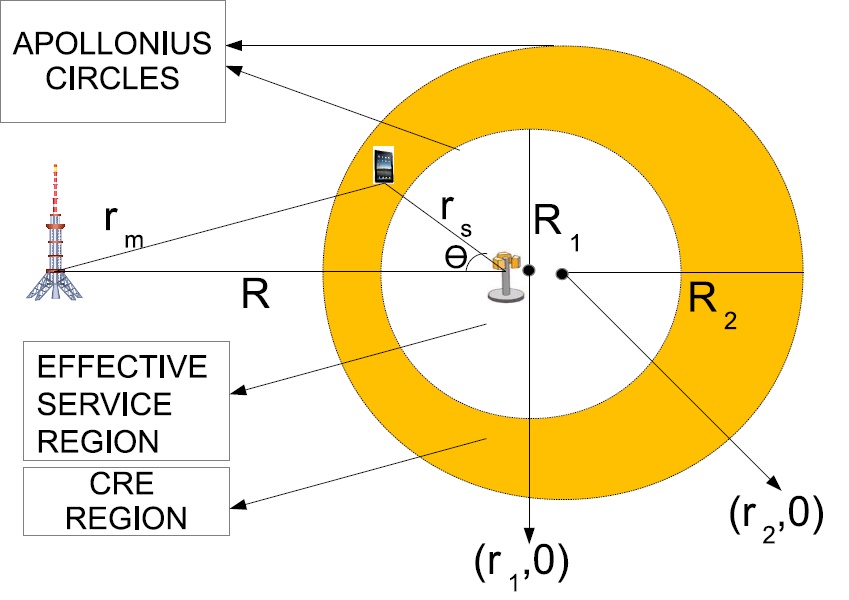
LTE-Advanced Networks and Beyond:
The graphic alongside depicts a heterogenous network with a macro cell, and a small cell. The region within the two circles is the cell range extension region. I worked on innovations on LTE-Advanced (LTE-A) macro-cell deployments to improve system performance using optimized CA and eICIC techniques. I further propose an
outage mitigation framework for LTE-A wireless
networks, where we perform a dual optimization of the transmission
power and beamforming weight parameters at each neighbor
cell sector of the outage eNBs, while taking into account both
the channel characteristics and residual eNB resources, after
serving its current traffic load. Our interest lies in recent research in wireless, including but not limited to massive MIMO and spectrum sharing.
- A. Ghosh, V. Aggarwal, and P. Chakraborty, "Tiered Spectrum Measurement Markets for joint Licensed and Unlicensed Secondary Access," IEEE Transactions on Network Science and Engineering, vol. 7, no. 3, pp. 1295-1309, 1 July-Sept. 2020.
- K. Liu, Z. Zha, W. Wan, V. Aggarwal, B. Fu, and M. Chen, "Optimizing TCP Loss Recovery Performance Over Mobile Data Networks," IEEE Transactions on Mobile Computing, vol. 19, no. 6, pp. 1401-1419, June 2020.
- A. Elgabli, A. Elghariani, V. Aggarwal, and M. Bell, "A Low Complexity Detection Algorithm For Uplink Massive MIMO Systems Based on Alternating Minimization," Wireless Communications Letters, vol. 8, no. 3, pp. 917-920, June 2019.
- A. Elgabli, A. Elghariani, V. Aggarwal, M. Bell, and M. Bennis, "A Proximal Jacobian ADMM Approach for Fast Massive MIMO Detection in Low-Latency Communications," in Proc. IEEE ICC, May 2019.
- Anis Elgabli, Ali Elghariani, Vaneet Aggarwal, and Mark R. Bell, "QoE-Aware Resource Allocation for Small Cell," in Proc. Globecom, Dec 2018.
- A. Ghosh, R. Berry, and V. Aggarwal, "Spectrum Measurement Markets for Tiered Spectrum Access," IEEE Transactions on Cognitive Communications and Networking, vol. 4, no. 4, pp. 929-941, Dec. 2018.
- A. Ghosh, R. Berry, and V. Aggarwal, "Tiered Spectrum Measurement Markets for Licensed Secondary Spectrum", in Proc. International Conference on NETwork Games, COntrol and OPtimisation (NETGCOOP), Nov 2018.
- R. Sivaraj, I. Broustis, N. K. Shankaranarayanan, V. Aggarwal, R. Jana, and P. Mohapatra, "A QoS-enabled Holistic Optimization Framework for LTE-Advanced
Heterogeneous Networks," in Proc. 2016 IEEE Conference on Computer Communications (INFOCOM).
- R. Sivaraj, I. Broustis, N. K. Shankaranarayanan, V. Aggarwal, and P. Mohapatra, "Mitigating Macro-Cell Outage in LTE-Advanced Deployments," in Proc. 2015 IEEE Conference on Computer Communications (INFOCOM), pp.1284-1292, April 26 2015-May 1 2015.
Two-Sender Unicast Index Coding Problem:
The problem of two-sender unicast index coding consists of two senders and a set of receivers. Each receiver demands a unique message not demanded by any other receiver and has a subset of messages as its side information. Every demanded message is available with at least one of the senders. The senders avail the knowledge of the side information at all the receivers to reduce the total number of transmissions required to satisfy the demands of all the receivers. The objective is to find the minimum total of number of transmissions per message length (known as the optimal broadcast rate with finite length messages) and its limiting value as the message length tends to infinity (called the optimal broadcast rate). We provide the optimal linear
broadcast rates and corresponding code constructions for all the
possible cases of the two-sender unicast index coding problem
with fully-participated interactions. The optimal linear broadcast
rate and the corresponding code for the two-sender problem are
given in terms of those of the three single-sender unicast problems
associated with the two-sender problem. Further, going beyond linear, two-sender graph coloring is used to provide achievable broadcast rates for a class of the two-sender unicast index coding problem.
- Shanuja Sasi, Vaneet Aggarwal, and B. Sundar Rajan, "An Embedded Index Code Construction Using Sub-packetization," in Proc. IEEE Information Theory Workshop (ITW), Apr 2021.
- Chinmayananda Arunachala, Vaneet Aggarwal, and B. Sundar Rajan, "On the Optimal Broadcast Rate of the Two-Sender Unicast Index Coding Problem with Fully-Participated Interactions," IEEE Transactions on Communications, vol. 67, no. 12, pp. 8612-8623, Dec. 2019.
- Chinmayananda Arunachala, Vaneet Aggarwal, and B. Sundar Rajan, "Optimal Linear Broadcast Rates of Some Two-Sender Unicast Index Coding Problems," IEEE Transactions on Communications, vol. 67, no. 6, pp. 3965-3977, June 2019.
- Chinmayananda Arunachala, Vaneet Aggarwal, and B. Sundar Rajan, "Optimal Broadcast Rate of a Class of Two-Sender Unicast Index Coding Problem,," in Proc. IEEE ITW, Aug 2019.
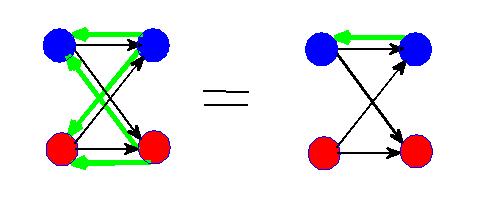
Feedback and Cooperation in Interference Channels:
I analyzed the role of feedback in the simple two-user interference channel shown in the graphic on the right. As a rule, the sum capacity of a network grows with the number of feedback links, but in this case I proved that dedicated feedback along a single direct link gives the same sum capacity as dedicated feedback along all four reverse links. I also looked at two-way communication and showed that when the interference is strong, it is optimal to operate the forward and feedback channels independently. Further, we look at general MIMO Interference Channels with feedback, and receiver cooperation to characterize the approximate capacity and GDoF regions. In this case, we give an extension of the concept of private and public power levels studied for SISO case in Gaussian Han-Kobayashi region to a general MIMO channel.
- M. Ashraphijuo, V. Aggarwal and X. Wang, "On the Symmetric K-user Interference Channels with Limited Feedback," IEEE Trans. Inf. Th., vol. 62, no. 12, pp. 6969-6985, Dec. 2016.
- M. Ashraphijuo, V. Aggarwal and X. Wang, "On the Symmetric K-user Interference Channels with Limited Feedback," in Proc. Allerton, Oct 2014.
- M. Ashraphijuo, V. Aggarwal and X. Wang, "On the Capacity and Degrees of Freedom Regions of MIMO Interference Channels with Limited Receiver Cooperation," IEEE Trans. Inf. Th., Vol. 60, no. 7, Jul 2014.
- M. Ashraphijuo, V. Aggarwal and X. Wang, "Degrees of Freedom Region for MIMO
Interference Channel with Limited Receiver Cooperation," in Proc. Allerton, Oct 2013.
- M. Ashraphijuo, V. Aggarwal and X. Wang, "On the Capacity Region and the
Generalized Degrees of Freedom Region for MIMO Interference Channel with Feedback," IEEE Trans. Inf. Th., vol. 59, no. 12, pp.8357-8376, Dec. 2013.
- A. Sahai, V. Aggarwal, M. Yüksel and A. Sabharwal,
"Capacity of All Nine Models of Channel Output Feedback for the Two-User Interference Channel," IEEE Trans. Inf. Th, vol. 59, no. 11, pp. 6957--6979, Nov 2013.
- M. Ashraphijuo, V. Aggarwal and X. Wang, "Generalized Degrees of Freedom Region
for MIMO Interference Channel with Perfect Feedback," in Proc. IEEE ISIT, Jul 2013.
- A. Sahai, V. Aggarwal, M. Yüksel and A. Sabharwal,
"Sum Capacity of General Deterministic Interference Channel with Channel Output Feedback," in Proc. IEEE ISIT, Austin, Jun 2010.
- A. Sahai, V. Aggarwal, M. Yüksel and A. Sabharwal,
"On Channel Output Feedback in Deterministic Interference Channels," in Proc. IEEE ITW, Taormina, Sicily, Oct. 2009.
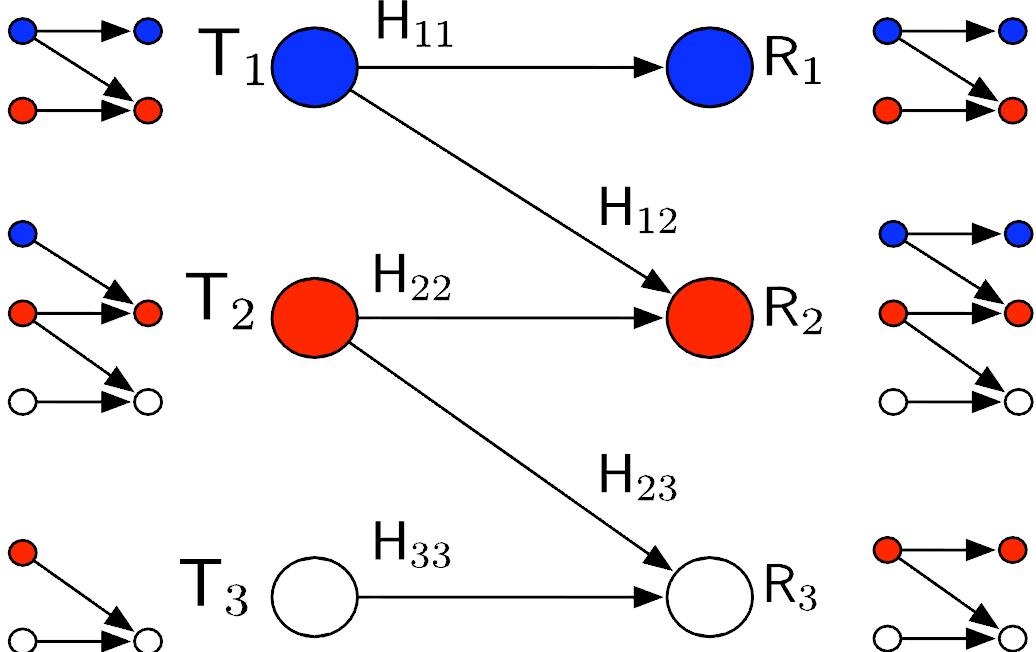
Local Algorithms that meet Global Performance Objectives:
The graphic alongside depicts a simple wireless network where each node is only aware of channel gains at nodes in its immediate neighborhood. Given only this local knowledge, I showed that there is no distributed algorithm that achieves the same sum capacity as the centralized algorithm. However, there exists a distributed algorithm that achieves the same sum capacity as the centralized algorithm if the top transmitter and receiver is given knowledge of two more hops. I used graph theory to explore the existence of a distributed optimal strategy for any topology with local knowledge at all the nodes. I also analyzed the effect of side information such as source arrival statistics and instantaneous queue state on the stable throughput region for a multiple access channel.
- A. Vahid, V. Aggarwal, S. Avestimehr, and A. Sabharwal, "Interference management with mismatched partial channel state information," EURASIP Journal on Wireless Communications and Networking, Aug 2017.
- P. Santacruz, V. Aggarwal, and A. Sabharwal, “Leveraging Physical Layer Capabilities: Distributed Scheduling in Interference Networks with Local Views,” IEEE/ACM Transactions on Networking, vol. 24, no. 1, pp. 368-382, Feb. 2016.
- P. Santacruz, V. Aggarwal, and A. Sabharwal, “Beyond Interference Avoidance: Distributed Sub-network Scheduling in Wireless Networks with Local Views,” in Proc. IEEE Infocomm, 2013.
- A. Vahid, V. Aggarwal, S. Avestimehr, and A. Sabharwal, “On the Capacity of Multi-Hop Wireless Networks with Partial Network Knowledge,” in Proc. Allerton, Sept. 2010.
- V. Aggarwal, S. Avestimehr, and A. Sabharwal, “On Achieving Local View Capacity Via Maximal Independent Graph Scheduling,” Special Issue of the IEEE Transactions on Information Theory on Interference Networks, May 2011.
- V. Aggarwal,
S. Avestimehr and A. Sabharwal, “Sum-Capacity of Interference Networks with Partial Information,” in Proc. IEEE ISIT, Austin, Jun 2010.
- V. Aggarwal, S. Avestimehr, and A. Sabharwal, “How (Information Theoretically) Optimal Are Distributed Decisions?,” in Proc. IEEE CISS, Mar 2010.
- V. Aggarwal, S. Avestimehr, Y. Liu, and A. Sabharwal, “Feedback via Message Passing in Interference Channels,” in Proc. IEEE ACSSC, Nov 2009, Pacific Grove, CA.
- V. Aggarwal, Y. Liu and A.
Sabharwal, “Sum-capacity of Interference Channels with a Local View: Impact of Distributed Decisions,” IEEE Trans. Inf. Th., Mar 2012.
- V. Aggarwal, L. Sankar, A. R. Calderbank and H. V. Poor,
“Ergodic Layered Erasure One-Sided Interference Channels,” in Proc. IEEE
ITW, Taormina, Sicily, Oct. 2009.
- V. Aggarwal,
S. Avestimehr and A. Sabharwal, “Distributed Universally Optimal Strategies in Wireless Networks,” in Proc. Allerton, Sept-Oct 2009.
- J. Xiao, V. Aggarwal, A. Sabharwal and Y. Liu, “Interference networks with local view: A distributed optimization approach,” in Proc. Forty-Seventh Annual Allerton Conference on Communication, Control, and Computing, Sept-Oct 2009.
- V. Aggarwal,
Y. Liu and A. Sabharwal, “Message Passing in Distributed Wireless Networks,” in Proc. ISIT, Seoul, Korea, Jun.-Jul. 2009.
- V. Aggarwal
and A. Sabharwal, “Slotted
Gaussian Multiple Access Channel: Stable Region and Impact of Side
Information,” EURASIP special issue on Theory and Applications in
Multiuser/Multiterminal
Communications, Apr. 2008.
- V. Aggarwal, “Distributed Joint Source-Channel Coding for arbitrary memoryless correlated sources and Source coding for Markov correlated sources using LDPC codes,” arXiv:0802.2666v1, Feb 2008.
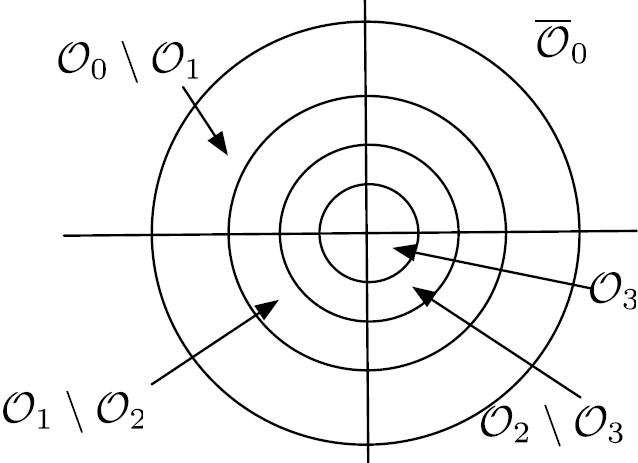
Multi-round Protocols for Two-way Fading Channels:
Most communication systems use some form of feedback, often related to channel state information. It is standard to assume perfect channel state information at the receiver or noiseless feedback links. With more realistic assumptions, the picture of what rates are possible changes dramatically. I was able to determine a diversity-multiplexing tradeoff that properly accounts for the errors in training the receiver and the errors in the feedback link for FDD (Frequency Division Duplexed) systems, where the forward and the feedback links are independent MIMO channels and for TDD (Time Division Duplexed) systems, where the forward and the feedback links have reciprocity. We break with the tradition in all current channel state based protocols by using multiple rounds of conferencing to extract more bits about the actual channel. This iterative refinement of the channel increases the diversity order with every round of communication. The protocols
are on-demand in nature, using high powers for training and feedback only when the channel is in poor states. I showed for FDD systems that the diversity multiplexing tradeoff with perfect training and K levels of perfect feedback can be achieved, even when there are errors in training the receiver and errors in the feedback link, with a multi-round protocol which has K rounds of training and K-1 rounds of binary feedback. For TDD systems, I developed new achievable strategies with multiple rounds of communication between the transmitter and the receiver, which use the reciprocity of the forward and the feedback channel. The multi-round TDD protocol achieves a diversity-multiplexing tradeoff which uniformly dominates its FDD counterparts, where no channel reciprocity is available.
- V. Aggarwal and A.
Sabharwal, “Bits About the Channel: Multi-round Protocols for Two-way Fading Channels,” IEEE Trans. Inf. Th., June 2011
- V. Aggarwal and A.
Sabharwal, “Power-Controlled Feedback and Training for Two-way MIMO
Channels,” IEEE Transactions on Information Theory, vol.56, no.7, pp.3310-3331, July 2010.
- V. Aggarwal, G. G. Krishna, S. Bhashyam and A. Sabharwal, “Two Models
for Noisy Feedback in MIMO Channels,” in Proc. Asilomar Conference on Signals, Systems and Computers, Oct. 2008,
Pacific Grove, CA.
- V. Aggarwal
and A. Sabharwal, “Performance
of Multiple Access Channels with Asymmetric Feedback,” J-SAC
special issue on Exploiting
Limited Feedback in Tomorrow's Wireless Communication Networks,
vol. 26, issue 8, pp. 1516-1525, Oct. 2008.
- V. Aggarwal
and A. Sabharwal, “Diversity
Order Gain with Noisy Feedback in Multiple Access Channels,” in
Proc. International Symposium on Information Theory, pp.404-408, July 2008, Toronto.
- V. Aggarwal
and A. Sabharwal, “On Multiple Access
Channels with Asymmetric Feedback,” in Proc. International
Symposium on Information Theory, pp.399-403, July 2008, Toronto.
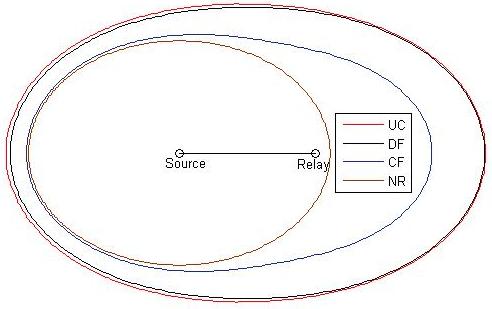
Relay Channels:
My work on wireless relay channels was partly sponsored by Siemens who were interested in how to deploy relays to provide a target rate to a given coverage area. I evaluated the coding strategies introduced by Cover and El Gamal that are known as Decode and Forward (DF) and Compress and Forward (CF). I showed that if the relay is able to decode, then DF is uniformly superior in that it provides coverage at any point served by CF. Further for any reasonable power ratio between the source and the relay, DF is superior. With Siemens, I also developed algorithms that enabled cooperative communication between Base Stations in two adjacent cells and a relay or a mobile station at the boundary of the two cells. I showed that phase-faded dirty-tape techniques (a causal modification of dirty-paper) have the potential to dramatically increase throughput, but are sensitive to the accuracy of the partial CSI available to the transmitter.
- V. Aggarwal,
A. Bennatan and A. R. Calderbank,
"On
Maximizing Coverage in Gaussian Relay Channels,"
IEEE Trans. on Inf. Th., vol.55, no.6, pp.2518-2536, June 2009
- A. Bennatan, V.
Aggarwal, Y. Wu, A. R. Calderbank, J. Hoydis and A. Chindapol, "Bounds and lattice-based transmission strategies for the phase-faded dirty-paper channel," IEEE Transactions on Wireless
Communications, vol.8, no.7, pp.3620-3627, July 2009.
- V. Aggarwal,
A. Bennatan and A. R. Calderbank,
"On
Maximizing Coverage in Gaussian Relay Networks",
in Proc. Information Theory Workshop, July 2007, Bergen.
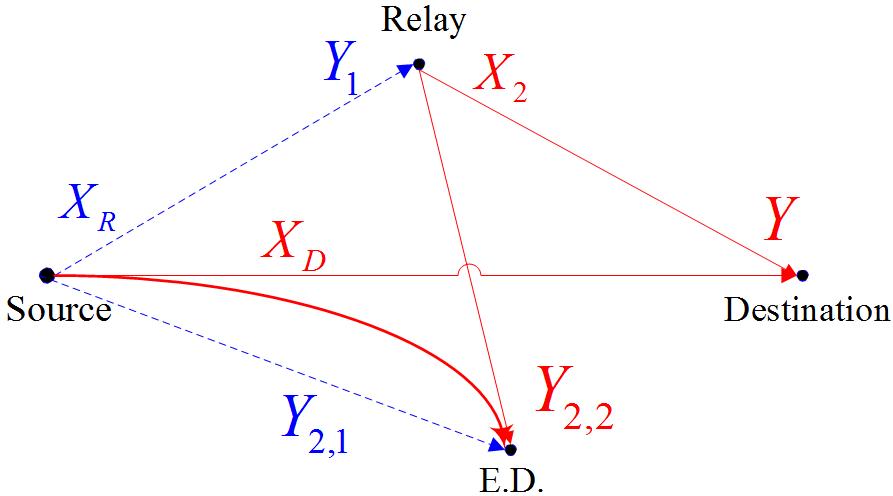
Secrecy Capacity:
I have analyzed the physical layer security provided by a relay network where the relay and destination receive signals on two orthogonal channels, and the eavesdropper can overhear either one or both of these channels. I proved that a partial decode and forward strategy is able to achieve the secrecy capacity. I have also evaluated the impact of an active eavesdropper who actively corrupts some of the bits in the channel from source to destination.
- S. Goel, V. Aggarwal, A. Yener and A. R. Calderbank, " The Effect of Eavesdroppers on Network Connectivity: A Secrecy Graph Approach," IEEE Transactions on Information Forensics and Security, vol.6, no.3, pp.712-724, Sept. 2011.
- S. Goel, V. Aggarwal, A. Yener and A. R. Calderbank, " Modeling Location Uncertainty for Eavesdroppers:
A Secrecy Graph Approach," in Proc. IEEE ISIT, Austin, 2010
- V. Aggarwal,
L. Sankar, A. R. Calderbank and H. V. Poor, "Secrecy
capacity of a class of orthogonal relay eavesdropper channels,"
EURASIP Journal on Wireless Communications and Networking,
Special Issue on Wireless Physical Layer Security, doi:10.1155/2009/494696, vol. 2009.
- V. Aggarwal,
L. Lai, A. R. Calderbank and H. V. Poor, "Wiretap channel II
with an active eavesdropper," in Proc. ISIT, Seoul, Korea, Jun.-Jul. 2009.
- V. Aggarwal,
L. Sankar, A. R. Calderbank and H. V. Poor, "Information Secrecy from Multiple Eavesdroppers in Orthogonal Relay Channels," In Proc.
ISIT, Seoul, Korea, Jun.-Jul. 2009.
- V. Aggarwal,
L. Sankar, A. R. Calderbank and H. V. Poor, "Secrecy capacity
of a class of orthogonal relay eavesdropper channels", in Proc. ITA, Feb. 2009.
Work in Undergrad:
- V. Aggarwal, "On Variable to Fixed length codes, Source Coding and Rényi’s Entropy," B.Tech Thesis, Indian Institute of Technology Kanpur, Apr 2005.
- V. Aggarwal, "On Variable to Fixed length codes, Source Coding and Rényi’s Entropy," B.Tech Thesis Mid Report, Indian Institute of Technology Kanpur, Dec 2004.
- V. Aggarwal, "Software Solutions for Single Instruction Issue, In Order Processors," Project Report, Infoscience Record EPFL, infoscience.epfl.ch/record/87078/files/Aggarwal2004_1425.pdf, Jul 2004.
- S. Aguirre, V. Aggarwal and D. Mlynek, "A Standalone GCC-based Machine-Dependent
Speed Optimizer for Embedded Applications," Technical Report, Infoscience Record EPFL, infoscience.epfl.ch/record/87075/files/Aguirre2004_1416.pdf, July 2004.
Home







